
Circuit Theory and Applications
Performance Analysis of M-ary DPSK with SIMO in Ground-to-HAP FSO System in the Presence of Beam Wander and Scintillation
Studying the performance of communication systems is essential to establish a reliable and stable link with an acceptable quality of service and minimum amount of resources. This paper evaluates the ground to HAP FSO link that uses the M-ary differential phase-shift keying (MDPSK) modulation technique in the presence of turbulence and beams wandering. The performance is analyzed by comparing the Average Symbol Error Rate (ASER) with an applicable threshold of 10-4. The results confirmed that, when limiting the transmitted power to 33 dBm, which is consistent with a practical perspective, the
Enhancing Spectral Efficiency of Ground-to-HAP FSO System with Adaptive MASK in Presence of Beam-wander and AoA Fluctuation
High Altitude Platform Station or HAP is an indispensable component for the upcoming wireless communication technologies. This paper presents an evaluation of the performance of a Ground-to-HAP communication system using free-space optical (FSO) technology. The performance of the system is determined by three factors: channel state, pointing error, and angle-of-arrival (AoA) fluctuation. Accordingly, the modulated-Gamma distribution is used as a channel modeling of the Ground-to-HAP uplink communication to analyze the effect of turbulence and beam wandering on the channel state. In this paper

An Optimized Non-Invasive Blood Glucose and Temperature Body Measurement System
Diabetes is a disease in which the body does not adequately process food for energy production. Most of the food we consume is converted into glucose, or sugar, which our bodies use for energy. Moreover, the pancreas, which is an organ located near the stomach, produces insulin, a hormone that aids in the transport of glucose into our bodies' cells. Diabetes occurs when your body either does not produce enough insulin or does not use its own insulin the way it is supposed to. Sugars accumulate in your blood as a result of this. This is why diabetes is often referred to as "sugar". People with
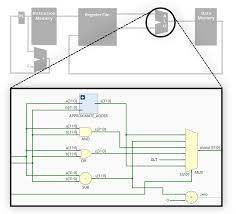
Single-Cycle MIPS Processor based on Configurable Approximate Adder
Enhancing computer architecture performance is a significant concern for architecture designers and users. This paper presents a novel approach to computer architecture design by using an approximate adder with configurable accuracy in a single-cycle MIPS processor as a study case. Using approximate adders decreased the delay on the expense of the design area. Using approximate computing with the MIPS processor, the timing performance has been improved by 253.4% compared to the lookahead adder. It has been implemented and tested using System-Verilog. © 2022 IEEE.
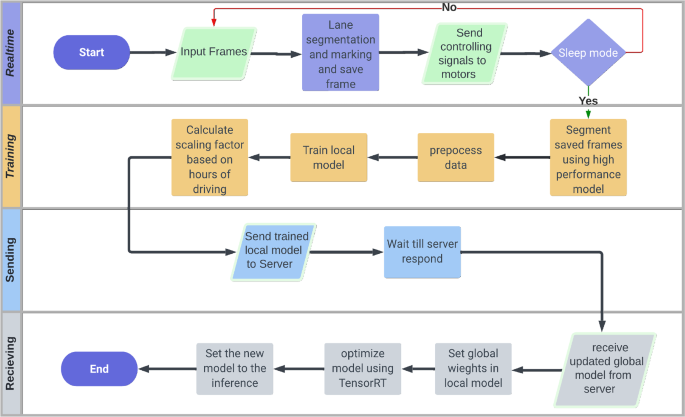
Federated learning system on autonomous vehicles for lane segmentation
Autonomous Vehicles (AV) is one of the most evolving industries in the last decade. However, one of the bottlenecks of this evolution is providing data that contains different scenarios and scenes to improve the models without exposing the privacy and security of the edge vehicles. The authors of this research propose a secure and efficient novel solution for lane segmentation in AVs through the use of Federated Learning (FL). FedLane involves initial training of U-Net, ResUNet, and ResUNet++ models, followed by real-time inference in edge devices and the application of FL to update the server
Cooperative MEC With Non-Uniform User Density: Resource Planning and State Control Optimization
Mobile edge computing (MEC) allows mobile devices to offload computationally intensive tasks to nearby base stations equipped with computational resources. MEC also provides a solution for supporting low latency responses. However, MEC increases the system power consumption by adding extra computational units. It is important to carefully plan computational resources to achieve a balance between quality of service (QoS) and power consumption. Moreover, the MEC system control should shut down unused resources when traffic rates fall to further decrease the power consumption. In this letter, we
SSHC with One Capacitor for Piezoelectric Energy Harvesting
Piezoelectric vibration energy harvesters have attracted a lot of attention as a way to power self-sustaining electronic systems. Furthermore, as part of the growing Internet of Things (loT) paradigm, the ongoing push for downsizing and higher degrees of integration continues to constitute major drivers for autonomous sensor systems. Two of the most effective interface circuits for piezoelectric energy harvesters are synchronised switch harvesting (SSH) on inductor and synchronous electrical charge extraction; nevertheless, inductors are essential components in both interfaces. This study
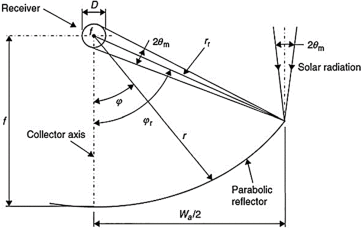
Investigative Review of Design Techniques of Parabolic Trough Solar Collectors
Parabolic trough solar collectors (PTCs) are among the most cost-efficient solar thermal technologies. They have several applications, such as feed heaters, boilers, steam generators, and electricity generators. A PTC is a concentrated solar power system that uses parabolic ref lectors to focus sunlight onto a tube filled with heat-transfer f luid. PTCs performance can be investigated using optical and thermal mathematical models. These models calculate the amount of energy entering the receiver, the amount of usable collected energy, and the amount of heat loss due to convection and radiation

Semi-Fragile Watermark for the Authentication and Recovery of Tampered Images
In order to strengthen the safety of corporate multimedia assets, a semi-fragile watermarking method is developed, which makes use of the integer wavelet transform (IWT) and the discrete cosine transform (DCT) for tamper detection and recovery. In this paper, we produce two distinct kinds of watermarks: an authentication watermark and a recovery watermark. A tamper detection methodology is utilized at the receiving end to check the watermarked image for validity and detect any assaults. If the changes are determined to be malicious, the suggested tamper recovery method is used to restore the

Providing a labeled statements dataset to enhance the trans-compilation-based tools
Nowadays Mobile Applications are a necessity as everyone is depending on them in their everyday tasks. We use them for communication, entertainment, and utilities. Every day new devices are introduced to the market. The diversity in these devices resulted in many platforms like Android and iOS. These different mobile platforms used by different companies and manufacturers made it challenging for mobile developersto build an application or a system that can be deployed on different platforms. Developers will be required to go through multiple development cycles to develop the application for