
Circuit Theory and Applications

Fractional Order Systems: An Overview of Mathematics, Design, and Applications for Engineers: Volume 1 in Emerging Methodologies and Applications in Modelling
Fractional Order Systems: An Overview of Mathematics, Design, and Applications for Engineers introduces applications from a design perspective, helping readers plan and design their own applications. The book includes the different techniques employed to design fractional-order systems/devices comprehensively and straightforwardly. Furthermore, mathematics is available in the literature on how to solve fractional-order calculus for system applications. This book introduces the mathematics that has been employed explicitly for fractional-order systems. It will prove an excellent material for

Fractional order systems: An overview of mathematics, design, and applications for engineers
Fractional Order Systems: An Overview of Mathematics, Design, and Applications for Engineers introduces applications from a design perspective, helping readers plan and design their own applications. The book includes the different techniques employed to design fractional-order systems/devices comprehensively and straightforwardly. Furthermore, mathematics is available in the literature on how to solve fractional-order calculus for system applications. This book introduces the mathematics that has been employed explicitly for fractional-order systems. It will prove an excellent material for
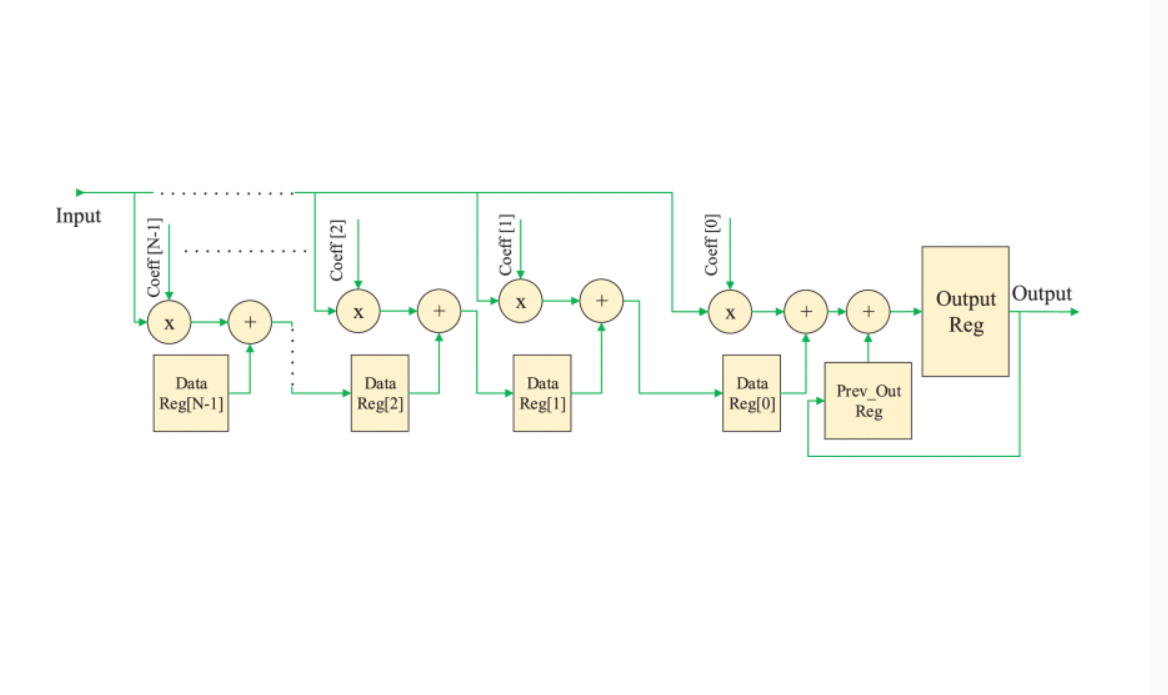
Hardware Accelerator of Fractional-Order Operator Based on Phase Optimized Filters With Applications
Hardware accelerators outperform CPUs in terms of performance by parallelizing the algorithm architecture and using the device’s programmable resources. FPGA is a type of hardware accelerator that excels not only in performance but also in energy efficiency. So, it provides a suitable platform for implementing complicated fractional-order systems. This paper proposes a novel phase-based optimization method to implement fractional operators using FIR and IIR filters. We also compare five fractional operator implementation methods on FPGA regarding resource utilization, execution time, power

Optimization of Double fractional-order Image Enhancement System
Image enhancement is a vital process that serves as a tool for improving the quality of a lot of real-life applications. Fractional calculus can be utilized in enhancing images using fractional order kernels, adding more controllability to the system, due to the flexible choice of the fractional order parameter, which adds extra degrees of freedom. The proposed system merges two fractional order kernels which helps in image enhancement techniques, and the contribution of this work is based on the study of how to optimize this process. The optimization of the two fractional kernels was done

A (k,n)-Secret Image Sharing With Steganography Using Generalized Tent Map
Secret Image Sharing (SIS) transfers an image to mutually suspicious receivers as n meaningless shares, where k or more shares must be present to recover the secret. This paper proposes a (k, n)-SIS system for any image type using polynomial interpolation based on Lagrange polynomials, where the generated shares are of size 1/k of the secret image size. A full encryption system, consisting of substitution and permutation stages, is employed by using the generalized Tent map as a source of randomness. In addition to using a long and sensitive system key, steganography using the Least

Double Visual Cryptography Using Generalized Tent Map, Rotation, and Image Filtering
This paper introduces a Multi-Visual Cryptography (MVC) system for sharing two color images, where the secrets can be revealed with low computation power using all the shares. The system uses the generalized Tent map as a source of randomness to generate any number of random shares. More specifically, (n-1) random shares are generated, and then, the nth share is calculated from the random shares and the secrets using rotations of the shares. In recovery, rotation of the last share recovers the two images based on the angle of rotation. Half the number of pixels is recovered for each secret

Progressive Multi-Secret Sharing of Color Images Using Lorenz Chaotic System
Multi-Secret Image Sharing (MSIS) systems share multiple images to multiple participants in unintelligible forms that can be recovered using all the shares. This paper employs the concept of progressive secret sharing with MSIS to introduce a new system, where the number of used shares in the recovery process defines the quality of the recovered secrets. The proposed system works for any number of secret color images, and is lossless when all the shares are present. The Lorenz chaotic system, which is numerically solved using Euler method, is used as source of randomness to encrypt the secret
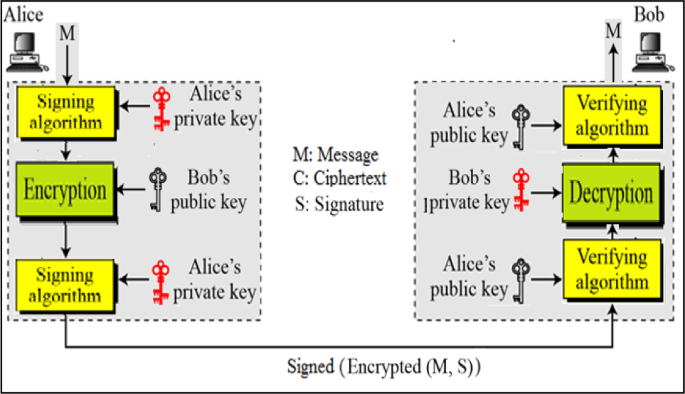
Networking and cryptography library with a non-repudiation flavor for blockchain
Blockchain is currently one of the most widely discussed inventions in the information and communication technology industry. It is a pillar of the fourth industrial revolution and it is a cryptographically demanding technology that is regarded as one of the most influential topics in academia. Many blockchain platforms currently utilize third-party cryptographic libraries that offer many cryptographic primitives in order to ensure users' protection against cyber-attacks. The Networking and Cryptography library (NaCl) is an open-source library for cryptographic primitives. NaCl is known to be

Interdigitated C-Patch Metamaterial Antenna for Terahertz Sensing
This paper proposes a metamaterial Terahertz sensor with detected sensitivity for biomedical applications. The proposed sensor consists of two interdigitated golden C-shaped structures on top of Teflon substrate that is backed by a gold layer. The absorption spectrum contains a peak resonance corresponding to the maximum absorption of the sensor. The proposed sensor has a maximum narrow-band absorption at 3.35 THz, with an average sensitivity of 2.256 THz/RIU and a quality factor of 22.3. The developed model is checked for the range of refractive index range between n= 1.3 to n= 1.4 to check
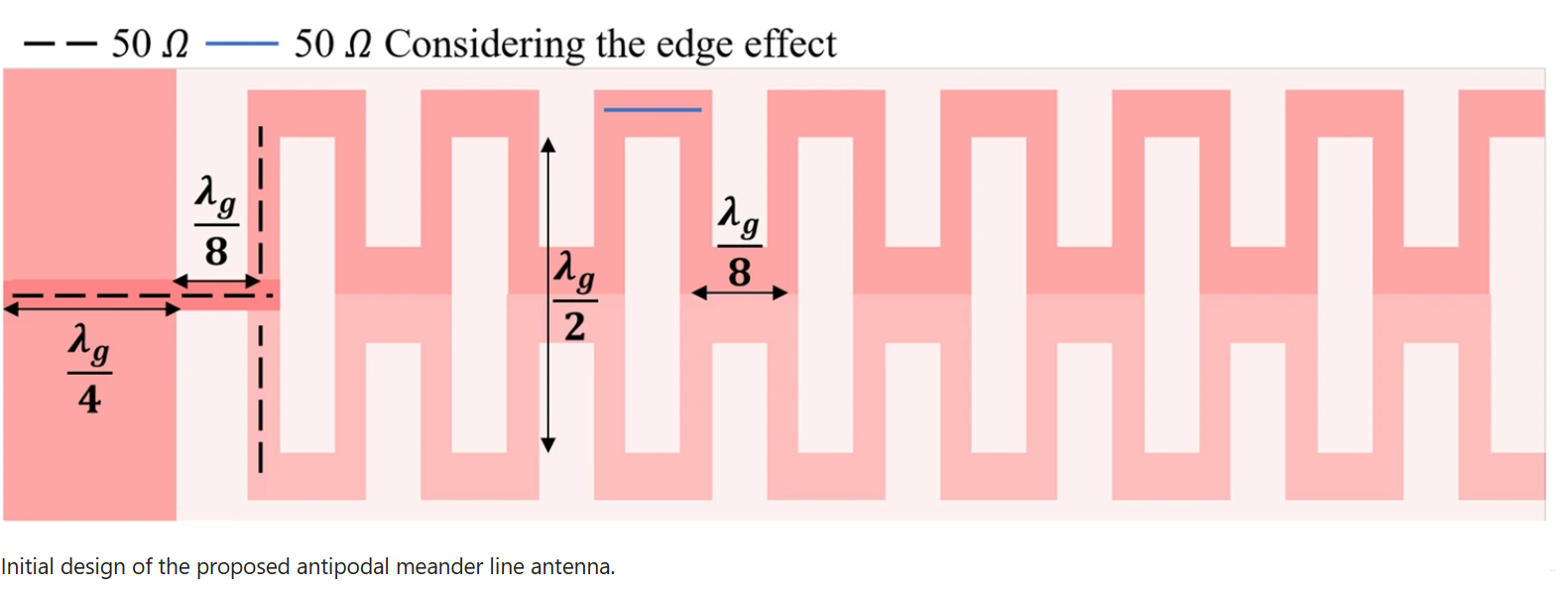
High gain antipodal meander line antenna for point-to-point WLAN/WiMAX applications
This paper introduces a planar antipodal meander line antenna fabricated using RO3003 substrate. The proposed antenna is designed to radiate in the end-fire direction, achieving a maximum measured gain of 10.43 dBi within its working bandwidth, which ranges from 2.24 GHz to 2.7 GHz, covering long-range WLAN/WiMAX applications. A systematic procedure is adopted in the design process to prove its tunability to cover other application requirements in terms of gain and bandwidth. The proposed design steps show that the bandwidth and the gain can independently be controlled by adjusting specific