
Circuit Theory and Applications
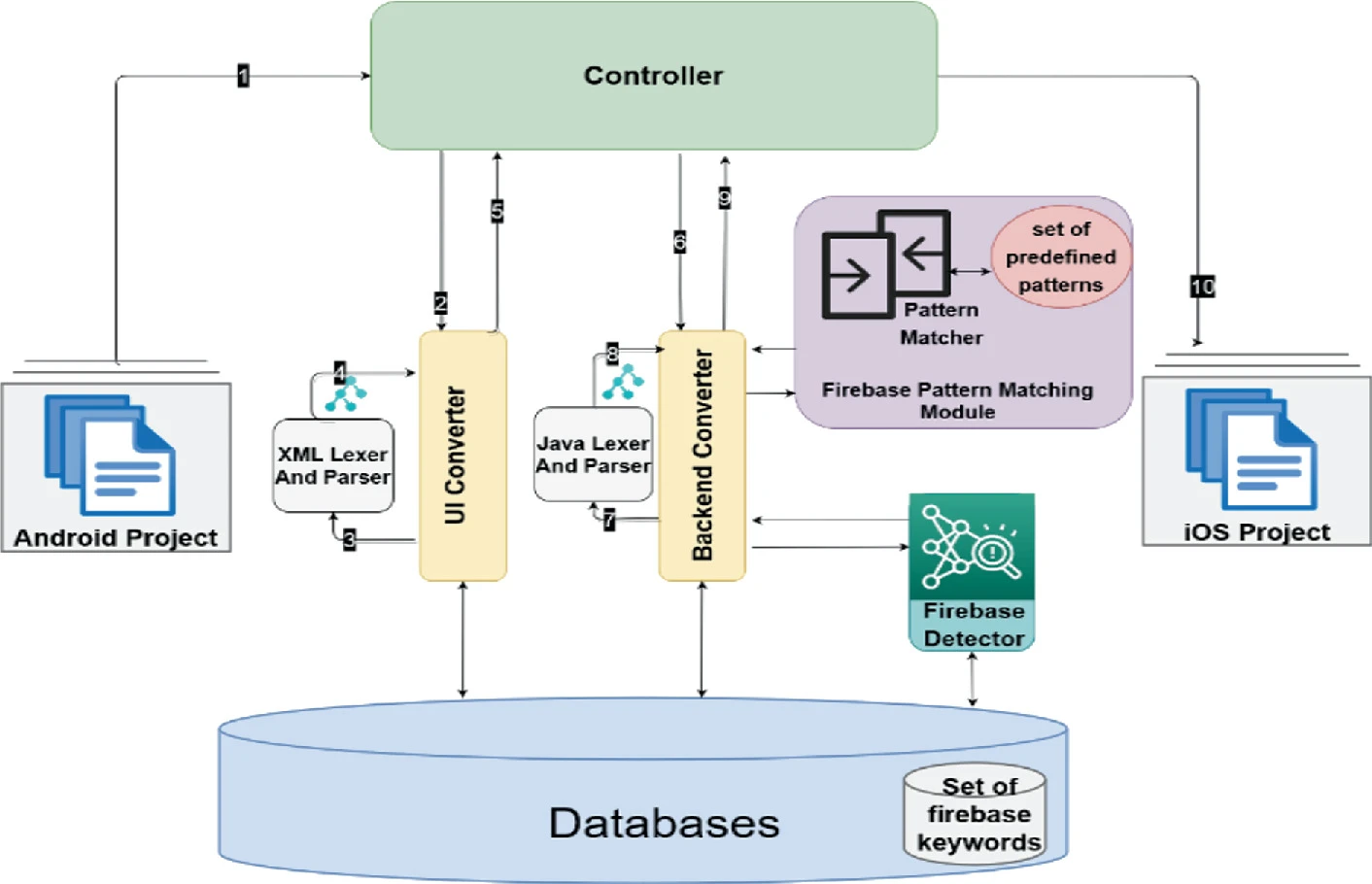
Trans-Compiler-Based Database Code Conversion Model for Native Platforms and Languages
Cross-platform mobile application development frameworks are now widely used among software companies and developers. Despite their time and cost-effectiveness, they still lack the performance and experience of natively developed applications. Many research tools have been proposed to solve this problem by converting a natively developed application from one platform to another. The Trans-Compiler Based Android to iOS Converter (TCAIOSC) was proposed to convert the front-end and back-end code of Android Java applications to iOS applications. Since databases are essential for mobile

Gold Price Prediction using Sentiment Analysis
Gold is one of the valuable materials that is used for funding trading purchases. Nowadays, more investors are interested in gold investments due to the sudden increase in gold prices. However, transactions involving gold are risky, the price of gold fluctuates wildly due to the unpredictability of the gold market. Hence, there is a need for the development of gold price prediction scheme to assist and support investors, marketers, and financial institutions in making effective economic and monetary decisions. This paper analyzes the correlation between gold price movements and sentiments of

Exploring State-of-the-Art Models in Arabic NLP: Insights into Multi-Label Text Classification
This study addresses the challenge of multi-label text classification in the Arabic language, focusing on movie genre categorization using plot summaries. Even though over 400 million people speak Arabic, its natural language processing (NLP) advances are not keeping up with those of other languages because of data shortages and quality difficulties. Three key contributions are made by this research to narrow this gap: a thorough analysis of prior research on Arabic multi-label text classification; the introduction of a newly curated dataset containing 22 genre labels for Egyptian movies; and
Feasibility Study of Using Predictive LTE Connection Selection from Multi-Operator for Teleoperated Vehicles
Service depending on good connection is growing and so its sensitivity, like Advanced Driver-Assistance System (ADAS). ADAS is the most common technological feature in the modern car, and the hope to reach a dependable anonymous car is the ultimate target. We (From end user and manufacture perspectives) are evaluating Teleoperated Driving as the most promising achievable feature to support emerging needs for traffic headache avoidance and health & safety cautions, with human to human sense & interaction proven to be better than Human to Machine in handling (Human driving vs. Machine driving)
Comparison of Different Deep Learning Approaches to Arabic Sarcasm Detection
Irony and Sarcasm Detection (ISD) is a crucial task for many NLP applications, especially sentiment and opinion mining. It is also considered a challenging task even for humans. Several studies have focused on employing Deep Learning (DL) approaches, including building Deep Neural Networks (DNN) to detect irony and sarcasm content. However, most of them concentrated on detecting sarcasm in English rather than Arabic content. Especially studies concerning deep neural networks, including convolutional neural networks (CNN) and recurrent neural network (RNN) architectures. This paper investigates

DevSecOps: A Security Model for Infrastructure as Code over the Cloud
DevSecOps includes security practice while applying DevOps. DevSecOps help secure the whole DevOps process. This paper aims to define a DevSecOps module to be used by the infrastructure team while applying infrastructure as code. The proposed module solves the problem of security by including security practice with the DevOps cycle to reach DevSecOps. The module was tested to measure time effi-ciency. A small survey was created to test other DevSecOps metrics and enhance future work. © 2022 IEEE.
Blockchain Application on Big Data Security
In recent years, advances in technology in several industries have resulted in massive data collections on the web. It raises worries about large data security and protection. The advent of Blockchain technology has caused a revolution in the security field for different applications. The distributed ledger is stored on each Blockchain node, which enhances security and data transparency. On the Blockchain network, illegal users are not authorized to undertake any fault transactions. In this article, we will discuss how Blockchain may be employed to secure the big data. We explain the problems
Blockchain in Healthcare for Achieving Patients' Privacy
Heath data are sensitive and valuable for individuals. The patients need to integrate and manage their medical data continuously. Personal Health Record (PHR) is introduced as a solution for managing their health information. It gives patients ownership over their medical data and provides physicians with realignment data. However, it does not achieve reliability, traceability, trust, nor security of patient control. Centralization of any data is vulnerable to the problem of hacking and single failure in addition to control from one organization. So, the centralization of data is the common
Topic Modeling on Arabic Language Dataset: Comparative Study
Topic modeling automatically infers the hidden themes in a collection of documents. There are several developed techniques for topic modeling, which are broadly categorized into Algebraic, Probabilistic and Neural. In this paper, we use an Arabic dataset to experiment and compare six models (LDA, NMF, CTM, ETM, and two Bertopic variants). The comparison used evaluation metrics of topic coherence, diversity, and computational cost. The results show that among all the presented models, the neural BERTopic model with Roberta-based sentence transformer achieved the highest coherence score (0.1147)
Smart Customer Care: Scraping Social Media to Predict Customer Satisfaction in Egypt Using Machine Learning Models
This paper proposes the utilization of posts from social media to extract and analyze customer opinions and sentiments towards any specified topic in Egypt. Summarized statistics and sentiment values are then displayed to the consumer (companies such as Vodafone, WE etc.) through both an attractive and functional user interface. Text, location, and time of thous and s of posts are scrapped, stored, preprocessed, then managed through topic modelling to infer all the hidden themes and delivered to a Recurrent Neural Network (RNN) to output whether the topic was positive or negative. Topic