
Circuit Theory and Applications
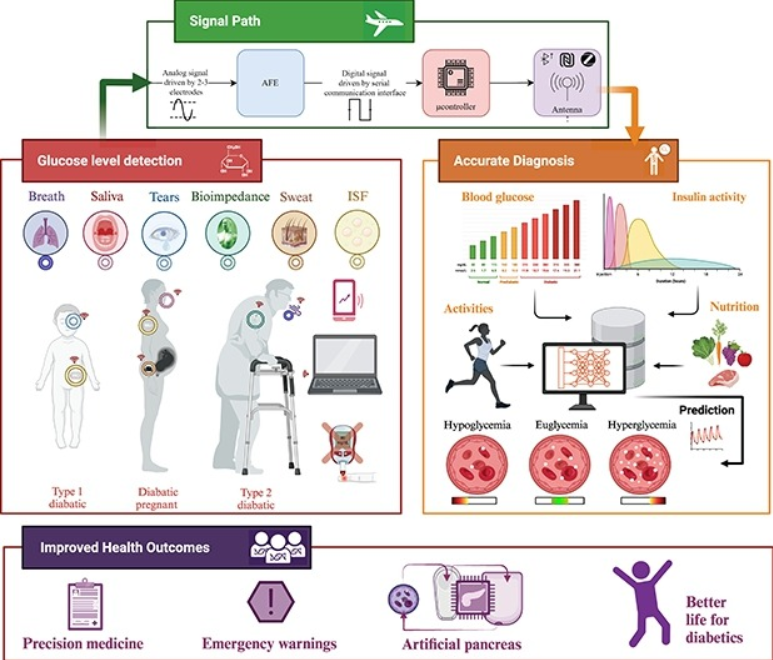
Wearable devices for glucose monitoring: A review of state-of-the-art technologies and emerging trends
Diabetes is a chronic condition that is characterized by high blood glucose levels and can cause damage to multiple organs over time. Continuous monitoring of glucose levels is essential for both diabetic and non-diabetic individuals. There have been major developments in glucose monitoring technology over the past decade, which have been driven by research and industry efforts. Despite these significant advancements, the area of glucose biosensors still faces significant challenges. This paper presents a comprehensive summary of the latest glucose monitoring technologies, including invasive
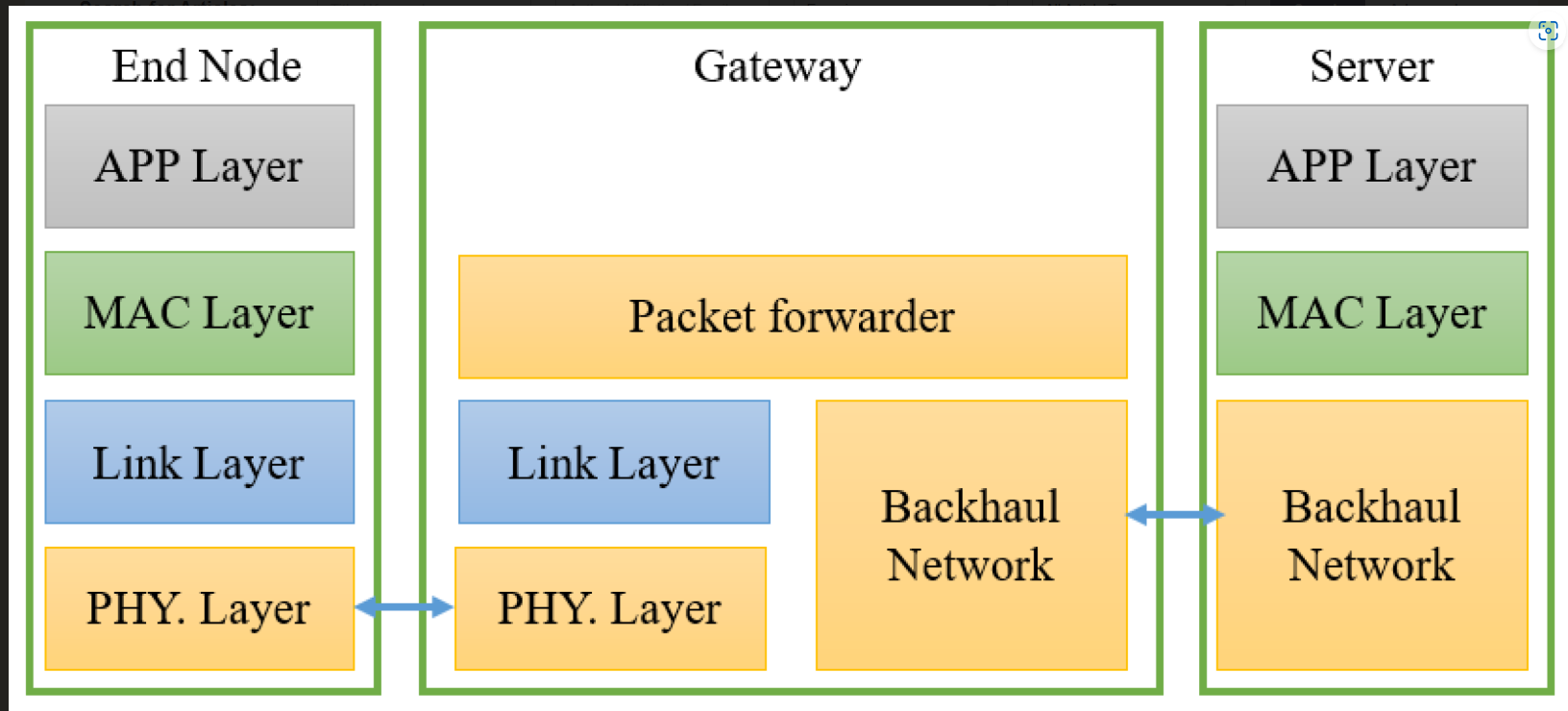
Internet of Things: A Comprehensive Overview on Protocols, Architectures, Technologies, Simulation Tools, and Future Directions
The Internet of Things (IoT) is a global network of interconnected computing, sensing, and networking devices that can exchange data and information via various network protocols. It can connect numerous smart devices thanks to recent advances in wired, wireless, and hybrid technologies. Lightweight IoT protocols can compensate for IoT devices with restricted hardware characteristics in terms of storage, Central Processing Unit (CPU), energy, etc. Hence, it is critical to identify the optimal communication protocol for system architects. This necessitates an evaluation of next-generation
Integrating Smart Contracts with WDNs Framework for Energy Management and Secure Transactions
The management of energy consumption and payment transactions using a secure, decentralized energy system framework is essential in the water distribution network (WDN). The water energy market, in which energy may be transformed into a digital asset that is potentially monitored, trackable and tradable, might greatly benefit from the deployment of blockchain technology. This is because the blockchain has transaction privacy, decentralization, security, and immutability features. Furthermore, using blockchain smart contracts enables energy market management operations such as consumers
Energy Optimization and Cost Reduction in Water Distribution Networks
Since the majority of energy consumed by water supply systems is used in transporting and distributing water, in addition to the energy required to pump the water from its sources, energy consumption is significantly associated with the water demand. Several studies have been carried out to optimize pump operations to achieve appropriate pressure and reduce the energy associated with controlling water levels in storage facilities. In this paper, we develop an optimization and decision support technique for a Water Distribution Network (WDN) that considers energy efficiency by limiting the

A Lightweight Image Encryption Scheme Using DNA Coding and Chaos
Protecting transmitted multimedia data such as images is a significant concern. This work proposes an encryption algorithm for greyscale images using a Pseudo-Random Number Generator (PRNG), DNA coding, and pixel sum. The proposed approach is implemented on a Genesys 2 FPGA using minimal hardware resources and can operate at a maximum frequency of 110.8 MHz. In addition, several performance evaluation tests are conducted for multiple images, including statistical analysis of the encrypted image, keyspace analysis, and differential attack analysis. The system is compared to recent works with
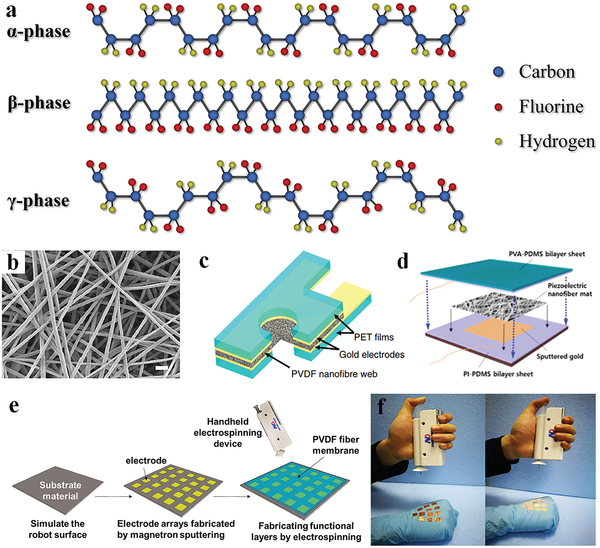
Improvement of piezoresistive pressure sensor using zig-zag shaped and PVDF material
Due to a wide range of applications in the biomedical industry, the need for flexible and wearable sensors is growing every day. A pressure sensor generates a signal based on the applied pressure. Sensors have become an integral component of our daily lives, from personal gadgets to industrial machinery. The identification of the low signal from the body necessitates the use of particularly sensitive sensors. The development of a pressure sensor that can transform the maximum input signal into an electrical output is critical. In this paper, zig-zag piezoresistors on a square diaphragm were
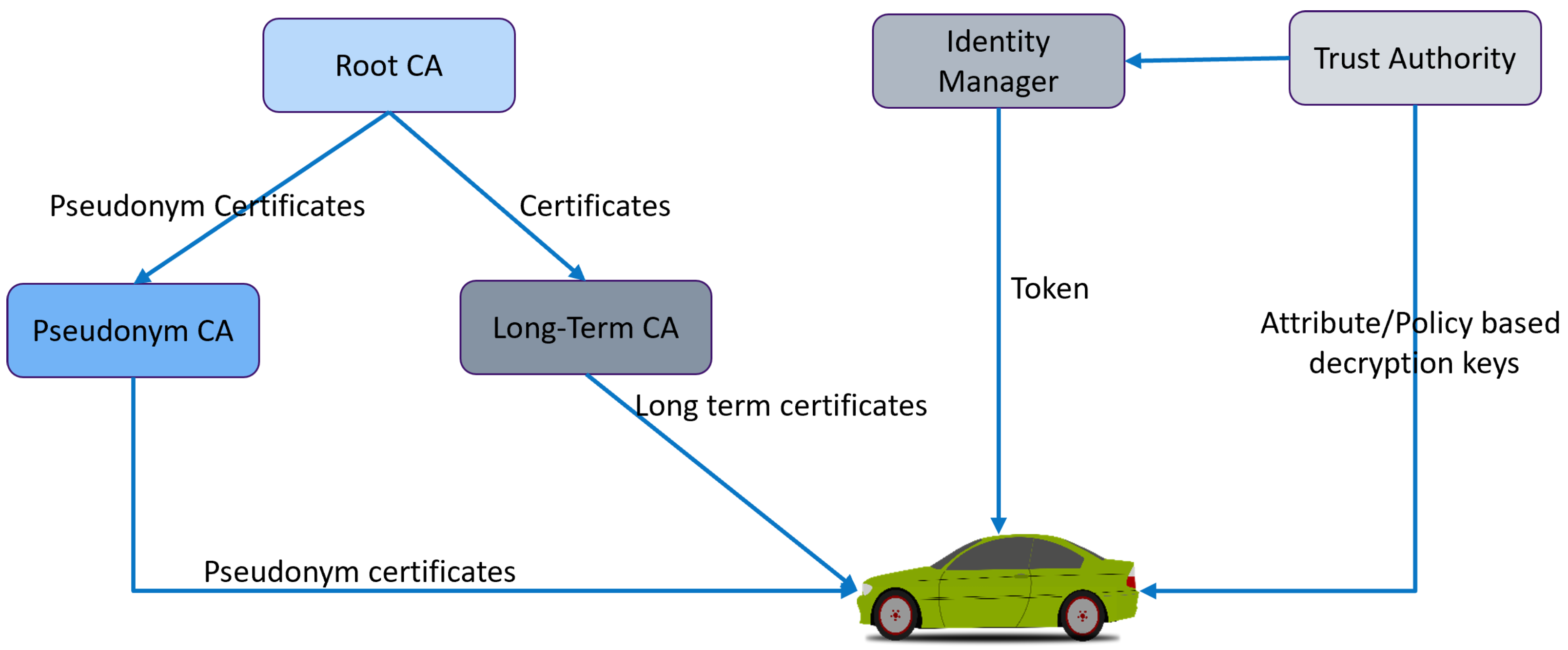
Developing Smart Control Platoon Algorithm for Secure VANET Environment
A vehicular ad hoc network (VANET) is a part of smart transportation. As a result of the vehicles being able to communicate with one another and share sensitive information, it is necessary to have an environment that can be trusted. Vehicles are clustered into platoons to ensure the secure transfer of information between them and select the platoon head of each platoon to control the vehicles. This paper proposes a smart control platoon system employing local and global trust schemes among vehicles in order to establish a secure environment. The platoon head calculates the local trust in each
Cross-Junction Based Metasurface for Wideband 90° Polarization Rotation
In this work, an ultrathin subwavelength metasurface based on a cross-junction-inspired unit cell that exhibits efficient wideband polarization rotation is presented. This structure manipulates the polarization of the incident electromagnetic radiation in the transmission band. The proposed metasurface converts the incident linearly polarized waves into the orthogonal polarization over a fractional bandwidth of 9.6% with a maximum insertion loss of 0.65 dB. The detailed analysis of the structure's inherent resonances and their origins are also presented with special emphasis on the intrinsic
Developing an Ultra-Dense Optical Frequency Comb Using an Integrated MZM and SPM Schemes in HNLF
Optical frequency comb (OFC) is a broad spec-trum comprised of closely spaced equidistant narrow lines. The generation of OFC is based on several nonlinear effects in highly nonlinear fiber (HNLF), which is employed to produce the repetitive frequencies. This work investigates the usage of cascaded Mach-Zehnder modulators (MZM) and self-phase modulation (SPM) in HNLF as effective spectrum broadening and comb generation techniques. Several parameters have been investigated in order to improve the output spectrum of the comb generation system. The parameters being investigated in this research
Qualitative Concentration Analysis of Glucose in a solution using Spectroscopic Measurement
Glucose concentration change in solution was recorded by studying transmission and absorption coefficient at different laser wavelengths, showing decrease in transmittance and increase in absorption coefficient due to increased glucose concentration. © Optica Publishing Group 2021, © 2021 The Author(s)