Indoor air pollution poses a substantial risk to human health and well-being, underscoring the crucial requirement for efficient monitoring systems. This paper introduces an advanced Air Pollution Monitoring System (APMS) tailored explicitly for indoor settings. The APMS integrates sensors and a user interface, ensuring the delivery of real-time and precise data concerning air quality parameters such as particulate matter (PM), volatile organic compounds (VOCs), carbon dioxide (CO2), as well as temperature and humidity. The proposed APMS has several advantages, including low maintenance

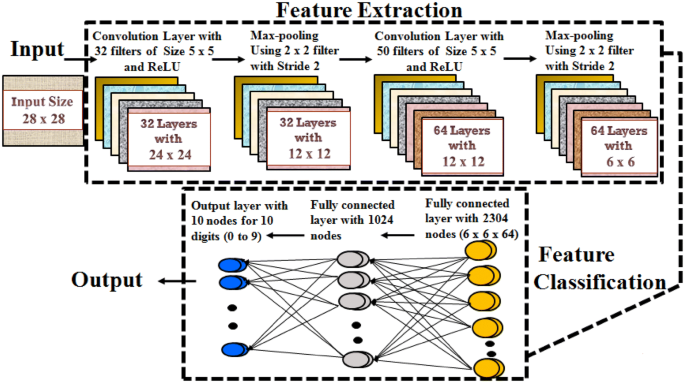
The process of giving machines the ability to recognize human handwritten digits and characters is known as handwritten digit and character recognition. Handwritten digits and characters are imperfect, vary from person to person, and can be constructed with a variety of flavors. Therefore, it's not a simple assignment for the machine. In this paper, a machine learning algorithm has been made to detect handwritten digits and characters with high accuracy relative to the past models. The MNIST dataset is used to provide the model with the training and test datasets for its variety of data

People's lives have been severely disrupted recently due to the COVID-19 outbreak's fast worldwide proliferation and transmission. An option for controlling the epidemic is to make individuals wear face masks in public. For such regulation, automatic and effective face detection systems are required. A facial mask recognition model for real-time video-recorded streaming is provided in this research, which categorizes the pictures as (with mask) or (without mask). A dataset from Kaggle was used to develop and assess the model. The suggested system is computationally more precise, efficient and

Digital Image Processing (DIP) is a growing field for various applications, such as autonomous vehicles and video surveillance. To improve the performance of DIP systems, image processing algorithms are implemented in hardware rather than software. The idea here is primarily to get a faster system than software imaging or other alternative hardware. Field-programmable gate arrays (FPGAs) have the advantages of parallel processing, low cost, and low power consumption. These semiconductor devices contain many logic blocks that can be programmed to perform everything from basic digital gate-level

This paper proposes a reliable wireless configuration bits programmer for remotely resetting incorrectly-written Microchip AVR microcontrollers' Fuses and Lock Bits. The incorrect configuration bits programming leads critically to a micro-controller malfunction which requires correct reprogramming. The proposed programmer utilizes Wi-Fi for enabling the remote configuration bits programming via a PC or a smart mobile device. It employs the Microchip AVR High Voltage Parallel and Serial Programming protocols which uniquely support the configuration bits programming feature. The configuration

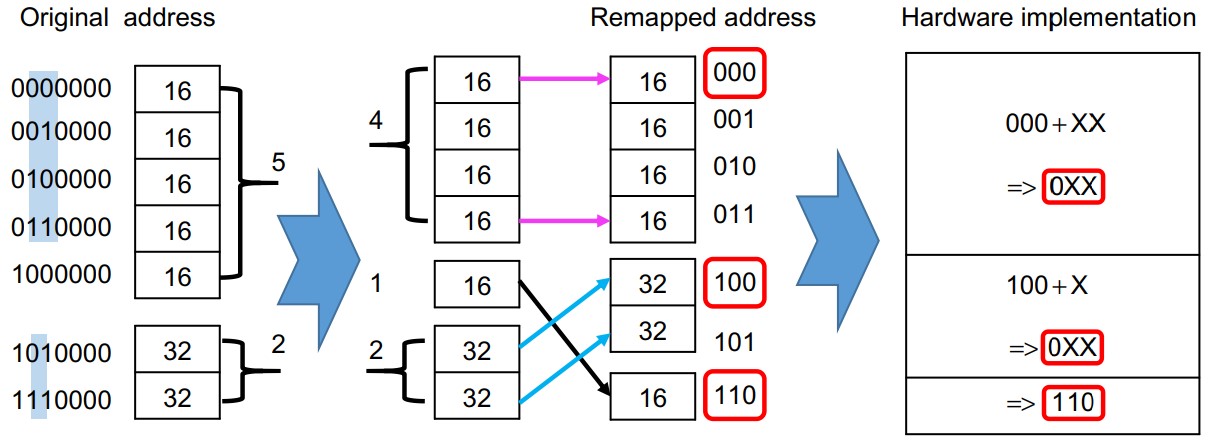
This chapter introduces two FPGA implementations of the fractional-order operators: the Caputo and the Grünwald-Letnikov (GL) derivatives. First, the Caputo derivative is realized using nonuniform segmentation to reduce the size of the Look-Up Table. The Caputo implementation introduced can generate derivatives of previously defined functions only. Generic and complete hardware architecture of the GL operator is realized with different memory window sizes. The generic architecture is used as a block to implement several fractional-order chaotic systems. The investigated systems include Borah

Deep neural networks (DNNs) are memory and computationally intensive; hence they are difficult to apply to real-time systems with limited resources. Therefore, the DNN models need to be carefully optimized. The solution was a model based on a convolutional neural network (CNN) called MobileNet that decreases the computational and space complexities with classification precision loss by utilizing depthwise separable convolutions. This study uses MobileNet vl architecture to improve image classification complexities to reach an acceptable complexity that can be used in real-time applications

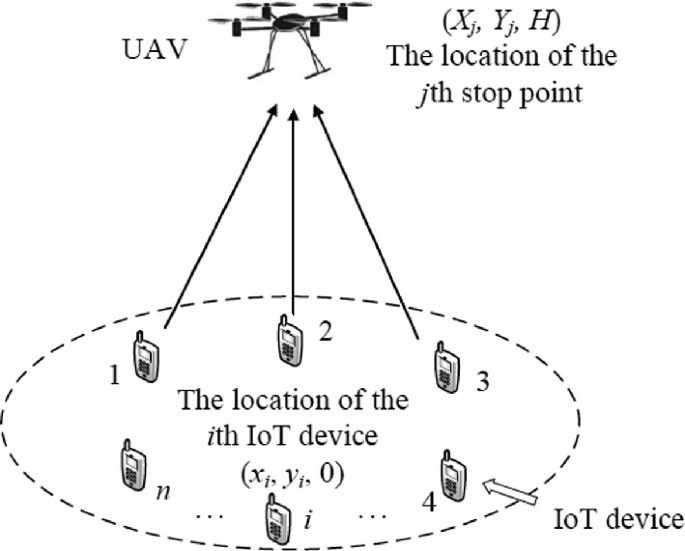
Unmanned aerial vehicles (UAVs) provide an energy-efficient and robust solution for data collection from the internet of things (IoT) devices. However, the UAV’s deployment optimization, including locations of the UAV’s stop points, is necessary to save the overall energy consumption and conduct the data collection efficiently. Thus, the objective is to minimize the energy consumption of the UAV and the IoT devices while collecting the data efficiently. This chapter proposes gaining-sharing knowledge (GSK) algorithm for optimizing the UAV’s deployment. In GSK, the number of UAV’s stop points

Floating point representations are required in many applications due to their universality and ability to represent huge numbers accurately and in compact bit-width. Floating point arithmetic is complex, performance inefficient, and area-consuming compared to integer arithmetic operations. In this paper, hardware realization of area-efficient high-performance floating point arithmetic units for IEEE 754 floating point single precision and double precision formats on FPGA are proposed. The proposed units achieved the same accuracy as software in all tested cases and were able to produce the

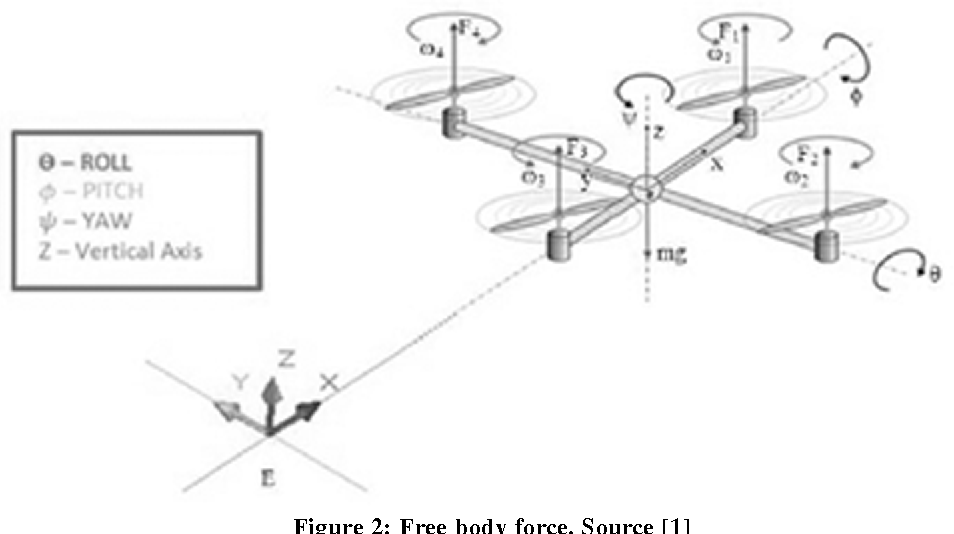
Unmanned Aerial Vehicle (UAV) technology is considered one of the important technologies at present, which is believed to solve many problems in the future, such as delivering small-weighted goods, agriculture, and civil fields. This research paper presents the mathematical model of a quadcopter that was developed as an example of an unmanned aerial vehicle. The MATLAB and Simulink environment create the model simulation and controller design. The present study proposes a cost-effective and easily deployable control system with a comparison that shows the difference between the controller made