
Circuit Theory and Applications

Modeling of light absorption in self-assembled truncated conical quantum dot structures
Quantum Dots have shown a significant potential as a top candidate for infrared photodetection at higher temperatures. In the presented work, a theoretical model for estimating the coefficient of optical absorption of self-assembled truncated conical quantum dot is developed. This model considers both bound-to-continuum and bound-to-bound absorption mechanisms that increase the accuracy of the absorption coefficient estimation. The developed model is based on estimating the bound states by diagonalizing the Hamiltonian matrix, where the density of states is computed using the Non-Equilibrium
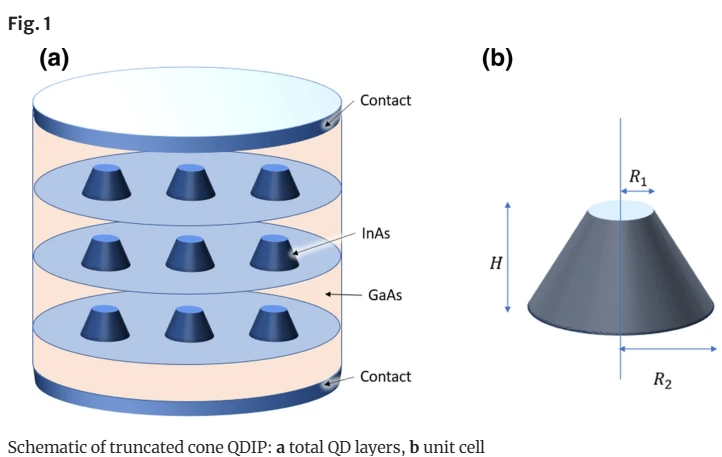
J–V characteristics of dark current in truncated conical quantum dot infrared photodetectors (QDIPs)
Quantum Dot Infrared Photodetector (QDIP) is one of the promising candidates for infrared photodetection due to its controllable heterojunction bandgap and sensitivity to normal incident radiation. It is expected to be superior to infrared photodetectors of mature technologies such as Mercury Cadmium Telluride (HgCdTe) or a quantum well infrared photodetector. In the presented paper, we have developed a theoretical model for the dark current in truncated conical QDIP as the truncated conical shaped QD structure is more appropriate to describe the fabricated dots. The dark current model is
A generalized framework for elliptic curves based PRNG and its utilization in image encryption
In the last decade, Elliptic Curves (ECs) have shown their efficacy as a safe fundamental component in encryption systems, mainly when used in Pseudorandom Number Generator (PRNG) design. This paper proposes a framework for designing EC-based PRNG and maps recent PRNG design techniques into the framework, classifying them as iterative and non-iterative. Furthermore, a PRNG is designed based on the framework and verified using the National Institute of Standards and Technology (NIST) statistical test suite. The PRNG is then utilized in an image encryption system where statistical measures
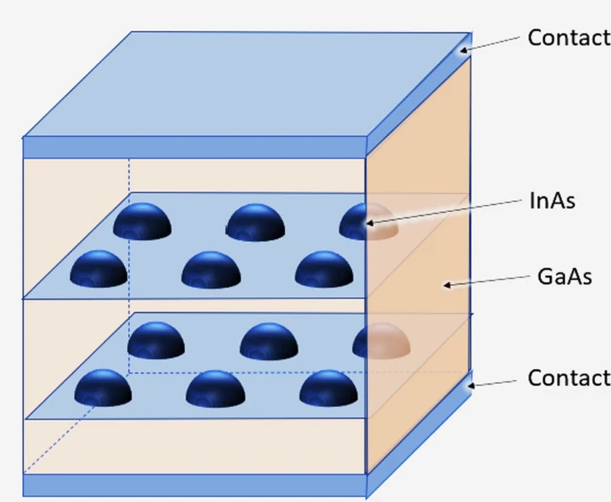
Modeling of dark current in semispherical quantum dot structures for infrared photodetection
Due to its tunable heterojunction bandgap and great sensitivity to normal incident illumination, the Quantum Dot Infrared Photodetectors (QDIPs) have received a lot of attention for the purpose of infrared sensing. It could be a very promising replacement for conventional infrared photodetectors made with established technology, including mercury cadmium telluride and quantum well infrared photodetectors. In this work, a model for the dark current in semispherical QDIP has been developed, resolves the primary semiconductor Poisson's and continuity equations, where the wave function and the
On the generalization of fractional-order transmission lines
This paper demonstrates some fundamentals concerning the study of the Fractional order Transmission Line (FTL) operation. A numerical algorithm applied to study the transient analysis is shown describing the abnormal diffusion that appears in the operation of the TL. According to the steady state analysis of the FTL operation, the superior advantages over the conventional domain of imposing the fractional parameters are shown in this work. Moreover, all the conventional formulas are retrieved from the corresponding fractional ones by setting all fractional derivatives to unity. © 2014 IEEE.

Microstrip Coupled Line Bandpass Filter: A Stochastic Model
Coupled line microstrip filter is regarded to be a strong contender for high frequency and wireless applications, due to its compact size, inexpensive cost, and simple engineering manufacturing. The stochastic study of the proposed microstrip filter, based on the Monte Carlo Model, presented in this paper explores the uncertainties in the microstrip filter's design parameters and their influence on the filter's functionality. The filter's microstrip thickness, lengths, and spacing are all considered as design factors. The analysis investigates the variation of the standard deviations, the mean
Nonlinear fractional order boundary-value problems with multiple solutions
It is well-known that discovering and then calculating all branches of solutions of fractional order nonlinear differential equations with boundary conditions can be difficult even by numerical methods. To overcome this difficulty, in this chapter two semianalytic methods are presented to predict and obtain multiple solutions of nonlinear boundary value problems. These methods are based on the homotopy analysis method (HAM) and Picard method namely, predictor HAM and controlled Picard method. The used techniques are capable of predicting and calculating all branches of the solutions

Wastewater Treatment: Recycling, Management, and Valorization of Industrial Solid Wastes
Wastewater Treatment: Recycling, Management, and Valorization of Industrial Solid Wastes bridges the gap between the theory and applications of wastewater treatments, principles of diffusion, and the mechanism of biological and industrial treatment processes. It presents the practical applications that illustrate the treatment of several types of data, providing an overview of the characterization and treatment of wastewaters, and then examining the different biomaterials and methods for the evaluation of the treatment of biological wastewaters. Further, it considers the various types of

Aloe Vera Tissue Modeling and Parameter Identification Using Meta-heuristic Optimization Algorithm
The agricultural industry's use of non-invasive bioimpedance monitoring methods is expanding quickly. These measured impedance fluctuations reflect imperceptible biophysical and biochemical changes in living and non-living tissues. Bioimpedance circuit modeling is a valuable method for fitting the measured impedance in biology and medicine. A study on two samples of Aloe Vera leaves is conducted to identify the best model representing Aloe Vera leaves, and two different interelectrode spacing distances are used to measure each sample. An electrochemical station (SP150) is used to detect bio

Energy Harvesting Management Unit for Wearable Devices
Energy harvesting materials and systems have become a popular study topic that is rapidly expanding. The harvesters will be used for a variety of applications, including distributed wireless sensor nodes for structural health monitoring, embedded and implanted sensor nodes for medical applications, recharging large system batteries, monitoring pressure in automobiles, powering unmanned vehicles, and running security systems in domestic settings. Components and devices at micro-macro sizes, spanning materials, electronics, and integration, have recently been developed. Energy harvesting has