
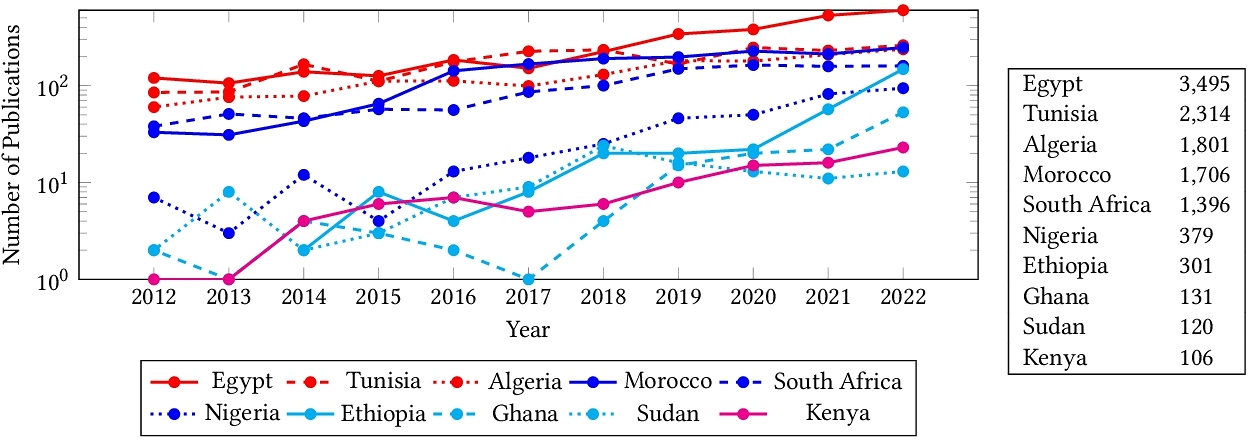
Despite significant efforts to democratize artificial intelligence (AI), computer vision which is a sub-field of AI, still lags in Africa. A significant factor to this, is the limited access to computing resources, datasets, and collaborations. As a result, Africa's contribution to top-tier publications in this field has only been 0.06% over the past decade. Towards improving the computer vision field and making it more accessible and inclusive, this study analyzes 63,000 Scopus-indexed computer vision publications from Africa. We utilize large language models to automatically parse their
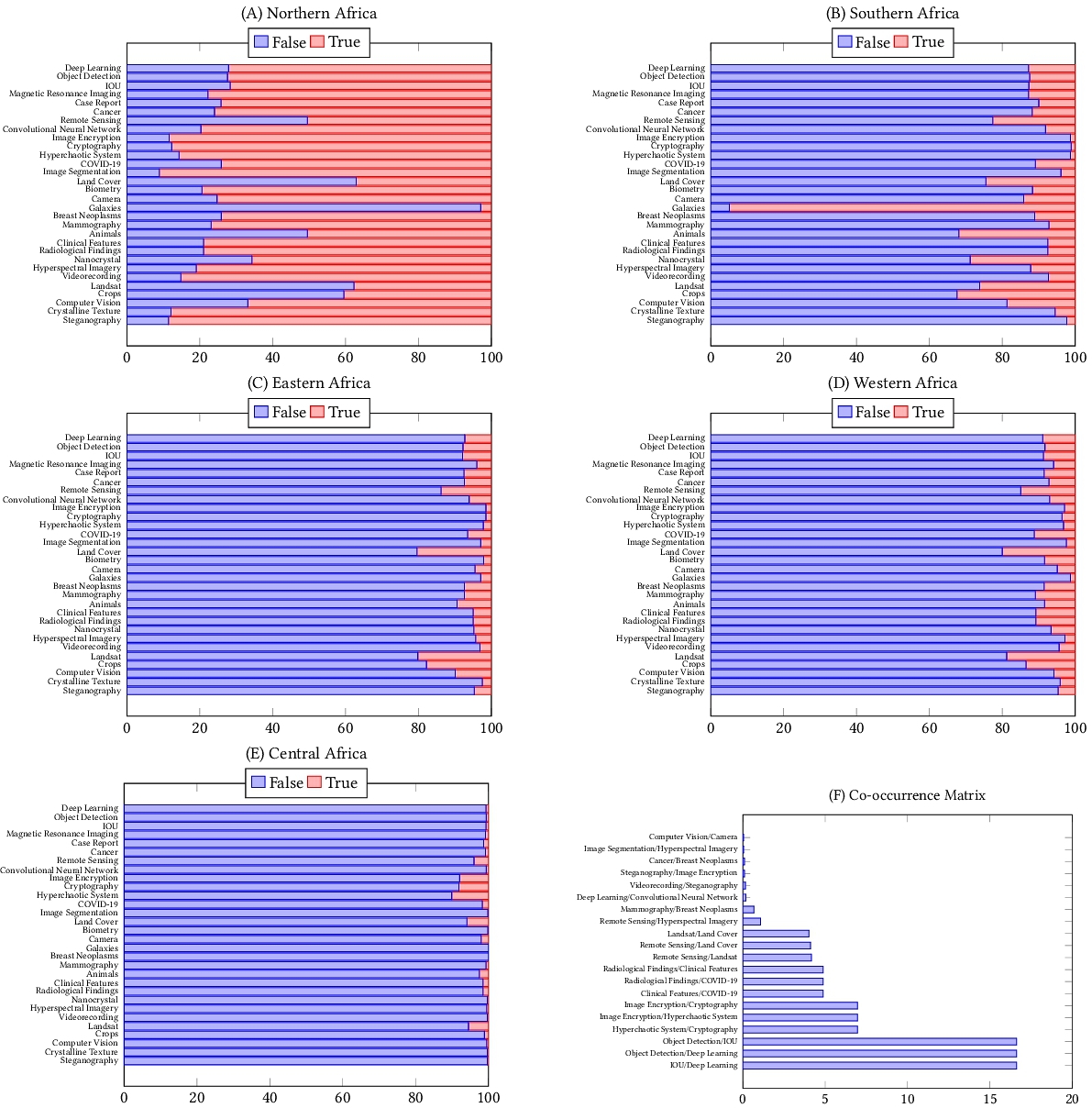
Computer vision is a broad field of study that encompasses different tasks (e.g., object detection, semantic segmentation, 3D reconstruction). Although computer vision is relevant to the African communities in various applications, yet computer vision research is under-explored in the continent and constructs only 0.06% of top-tier publications in the last ten years. In this paper, our goal is to have a better understanding of the computer vision research conducted in Africa and provide pointers on whether there is equity in research or not. We do this through an empirical analysis of the

Supply chain stages are known to be complex and variable. Variability and complexity increase due to the increased numbers of the stakeholders. Unified Modelling Language (UML) is known to be efficient in visualizing complex systems and highlighting both major and minor activities, hence provides stakeholders with better understanding and visualizing of the overall system. In this paper, UML models are developed and employed to model supply chain stages for a manufacturing firm. Functional, behavioral, and structural models are developed and explained throughout the paper. These UML models

Environmental concerns related to freight road transportation have been identified. Among the solutions to solve that problem is replacing conventional diesel-operated freight transportation vehicles with electric freight transportation vehicles. Although electric vehicles have a positive impact on environmental concerns, they have their challenges that make transportation companies reluctant to utilize them. In this paper, we address the challenges facing the transportation sector in replacing conventional diesel operated vehicles with electric ones in Egypt. Through PESTEL (political
In this work, the effects of adding hydrogen to diesel non-premixed combustion with air in a cylindrical furnace burner are investigated. A numerical model is developed to study the effects of hydrogen addition on combustion flame temperature and exhaust emissions. Different hydrogen addition ratios of 5%, 10%, 15%, and 20% by volume in the burning mixture are considered. The turbulence-chemistry interaction is modelled through the eddy dissipation combustion model to predict the concentration of exhaust emissions and the temperature of the combustion flame. The air-fuel equivalence ratio is

Holonomic robots are advantageous in several applications. The work presented in this paper performs the simulation of a 3 omni wheel mobile robot using MATLAB and V-REP. The simulated robot contains proximity sensors and cameras for obstacle detection and uses the Artificial Potential Field algorithm for path planning. The robot can map the surrounding environment while deviates and categorizes obstacles previously known or not. The results strongly suggest the effectiveness of the proposed methodology. © 2022 IEEE.

As the technological advancements in felid such as electronic, robotics, and artificial intelligence continue to grow and flourish, the more the traditional methods of doing things starts to get absolute. This phenomenon cannot be more clearly observed in like medicine, technological advancements changed the ways things are done from the way that the doctors preform their surgical operations to the way they prescribe pills and after surgery treatments. The purpose of this work is to develop a low-cost cable-driven manipulator robot to be used in the rehabilitation of human lower limb problems
This paper presents a comprehensive study on the optimization of PID controller parameters for a ball & plate system through the utilization of Genetic Algorithm (GA) and Particle Swarm Optimization (PSO). The objective of the study is to attain precise steady-state response while shortening settling time and minimizing overshoot. The assessment of controller performance is conducted using the Integral Absolute Error (IAE) cost function. The study highlights the limitations of conventional tuning techniques and the need for metaheuristic optimization algorithms, particularly when system models

A fault detection algorithm is proposed in this paper for wind farms. The algorithm is based on machine learning adopting Support Vector Machines (SVM). The focus is on the detection of grid faults for a Wind Farm of Doubly Fed Induction Generator (WF-DFIG). A high-fidelity model is used to simulate the system performance in faulty and healthy conditions. Statistical features based on steady-state signal analysis of measured signals are extracted. Machine learning results on a 9MW model WF-DFIG Grid-connected are provided by MATLAB/SIMULINK. The model performance is clarified and success in

A two-dimensional numerical model of tankless gas water heater (TGWH) is created to investigate the flow rate performance. The thermal and hydraulic performance for laminar flow over the water tube with different aspect ratios are studied numerically. The investigated variables are inlet hot air velocity and flat-tube aspect ratio. The Heat transfer coefficient from the present study is calculated and presented graphically. The results show that for input air velocities less than 1.5 m/s, the heat exchanger with the lower flat-tube aspect ratio provided a higher heat transfer coefficient; as