
Circuit Theory and Applications
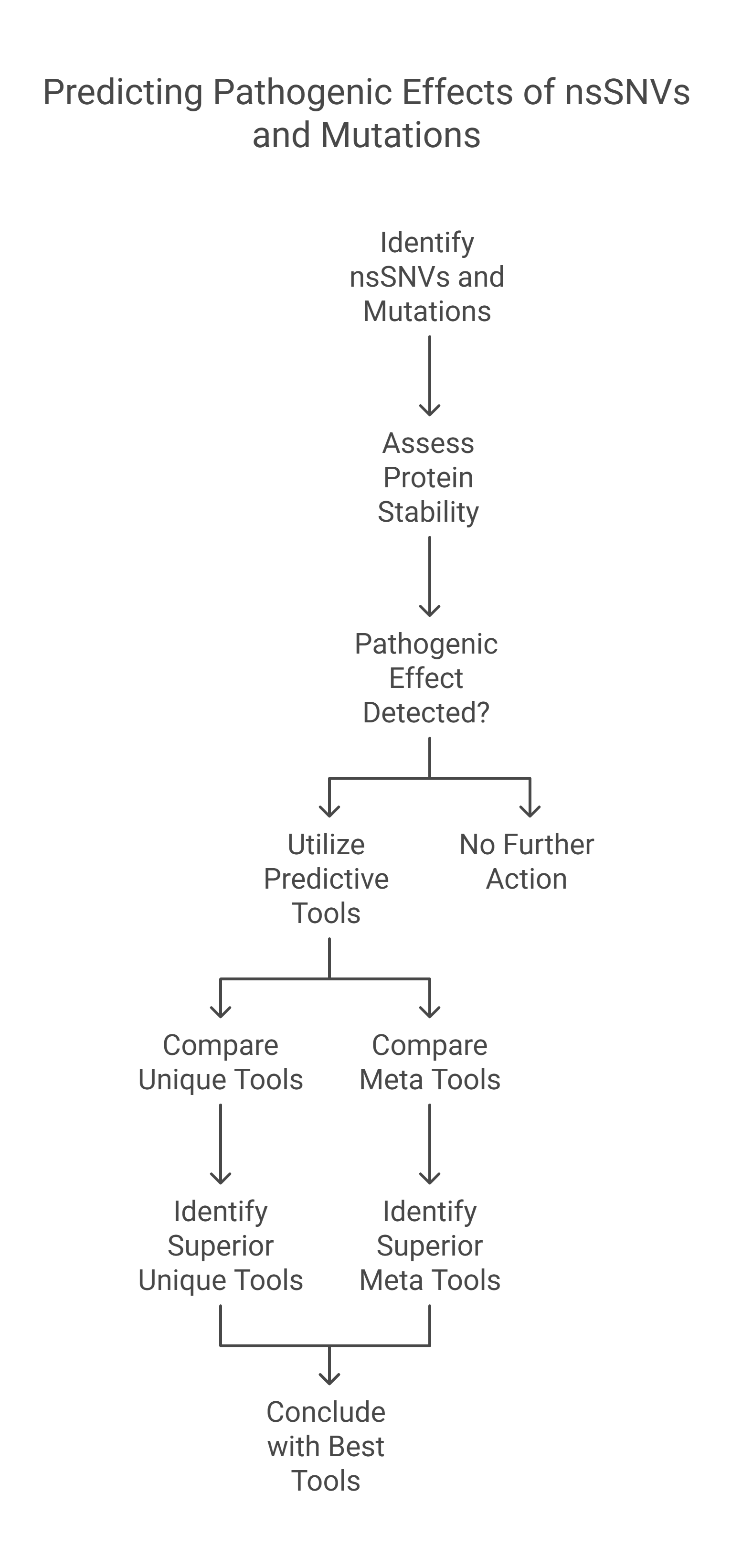
Predicting non-synonymous single nucleotide variants pathogenic effects in human diseases
Non-synonymous Single - Nucleotide Variants (nsSNVs) and mutations can create a diversity of the contrary influence of proteins like varying genotype and phenotype of any protein which affects its stability. The alterations in the protein stability may cause diseases. Detecting of nsSNVs and mutations can be a helpful tool in diagnosing diseases at an early stage. The study of singular and consensus tools for predicting pathogenic effects is very essential. Many studies utilized various predicting servers based on distinct Machine Learning Techniques (MLTs). In this research, we conduct a

Coffee and multiple sclerosis (MS)
Multiple Sclerosis (MS) is a long-term autoimmune disorder affecting the central nervous system, marked by inflammation, demyelination, and neurodegeneration. While the exact cause of MS remains unknown, recent research indicates that environmental factors, particularly diet, may influence the disease's risk and progression. As a result, the potential neuroprotective effects of coffee, one of the most popular beverages worldwide, have garnered significant attention due to its rich content of bioactive compounds. This chapter explores the impact of coffee consumption on patients with Multiple

Computational Intelligence for Medical Internet of Things (MIoT) Applications
Computational Intelligence for Medical Internet of Things (MIoT) Applications: Machine Intelligence Applications for IoT in Healthcare explores machine intelligence techniques necessary for effective MIoT research and practice, taking a practical approach for practitioners and students entering the field. This book investigates advanced concepts and applications in the MIoT field, guiding readers through emerging developments and future trends. A wide range of international authors guide readers through advanced concepts, including deep learning, neural network, and big data analytic
AI for Automated Thoracic Disease Assessment from X-Ray Imaging: a Review
With the increasing availability of digital X-ray imaging, artificial intelligence (AI) has emerged as a promising tool for automating the assessment of thoracic diseases. The objective of this study is to systematically review the artificial intelligence (AI) and deep learning methods proposed for the automated assessment of thoracic diseases from chest X-ray images. A thorough search of the relevant literature was conducted, and studies that met the inclusion criteria were critically reviewed. Information on the datasets, model architectures, evaluation metrics, and results was extracted
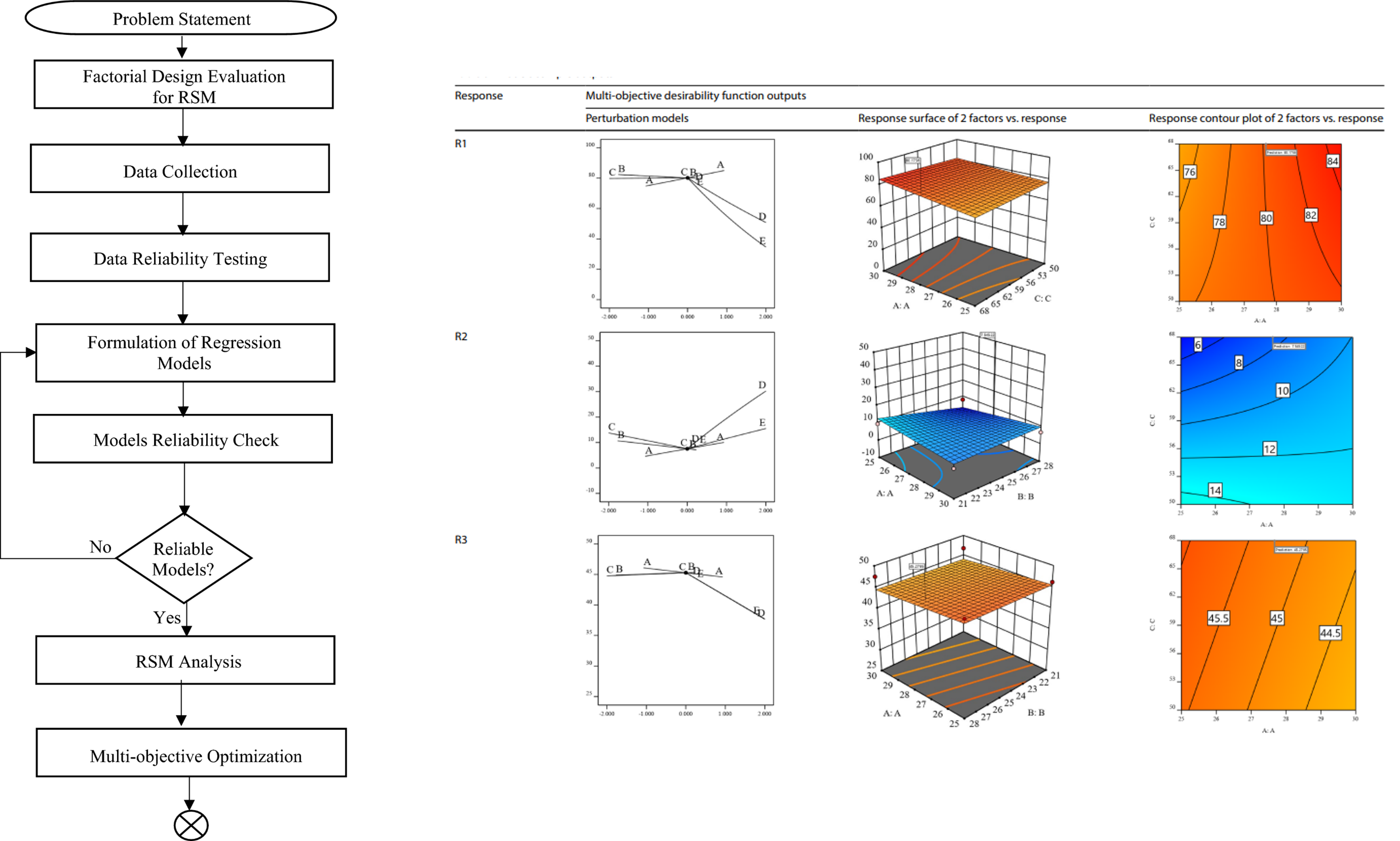
Multi-objective ergonomics design model optimization for micro electric cars via response surface methodology
Despite advancements in ergonomic comfort assessments in automotive design, optimizing seat dimensions within the constrained spaces of micro-electric cars presents a substantial challenge. In this study, response surface methodology (RSM) is utilized for the ergonomics design of a micro electric car in the conceptual design phase. Specifically, five critical seat dimensions are analyzed: Seatback Angle, Seat Base Angle, Steering Wheel Height from Car Base, Distance from Seat Base to Pedals, and Distance from Seat Base to Steering Wheel. The analysis took place using a 2-level full factorial
Hybrid Irrigation System in Egypt: Design and Optimization
This presents a hybrid photovoltaic/diesel system simulated as an alternative to the diesel generators required for water pumping systems. This hybrid system is designed to overcome the limitations of the fluctuating price and availability of diesel generators, ensure a reliable supply without interruptions, and improve the overall system efficiency. The system configuration offers an economical benefits over fully renewable hybrid systems or PV only systems. The novelty of the system design lies in minimizing its complexity in terms of design size and control while using a 10 KW photovoltaic
Product Mix Optimization Scenarios: A Case Study for Decision Support Using Linear Programming Approach
Determining the optimum product mix under the theory of constraints (TOC) has been considered by many researchers. In most cases, researches consider one scenario with one important aspect which is maximizing the profit by giving the best solution. This paper solves a product mix problem faced by a birds' food production facility. The problem is modeled and solved using two linear programing models. Several scenarios are presented for the same problem considering two important aspects, namely, resources' utilization and productivity. Data visualization is extensively used in this paper to
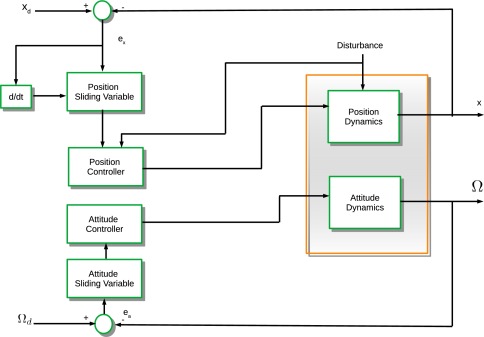
Robust fractional-order sliding mode control design for UAVs subjected to atmospheric disturbances
Trajectory tracking of unmanned aerial vehicles (UAVs) has been studied nowadays because it is necessary to design new controllers under different conditions. Severe atmospheric conditions are one of the major problems to overcome according to the path of the UAV. Conditions such as wind speed that can vary according to the weather conditions can affect the flight performance and of course in extreme cases can lead to stability problems. Some kinds of severe conditions are storms, snow, and hurricanes. These conditions are considered as disturbances in the roll, pitch, and yaw orientations of
Di- and tri- cyclic aromatic hydrocarbons removal using different prepared materials based Sargassum dentifolium algae, and iron oxide
Polycyclic aromatic hydrocarbons (PAHs) are highly toxic and carcinogenic compounds as they are low water solubility, hardly degradable and may persist in the environment for many years. Therefore, this study was directed to PAHs ‘anthracene and naphthalene’ removal using a combination method between adsorption and degradation using sunlight. Three adsorbent materials, iron oxide (Fe) alone, Sargassum dentifolium (S) alone, and mixture of Iron oxide and Sargassum dentifolium (FeS) were prepared. Afterwards, optimisation process was performed for the three adsorbent forms through some

Biological souring and mitigation strategies in oil reservoirs
Biological souring is one of the major problems facing the oil and gas sector as a result of biogenic sulfide generation in the reservoirs. Sulfidogenic microorganism and particularly sulfate-reducing bacteria are the main generator of the biogenic sulfide. In consequence, souring has a plethora of economic and environmental problems. It has a negative impact on the petroleum industry, where the generated sulfide lowers air quality and causes adverse health problems due to its toxicity and carcinogenicity. Furthermore, it affects the whole industry by reducing the product quality and enhancing