Self-excited attractors in jerk systems: Overview and numerical investigation of chaos production
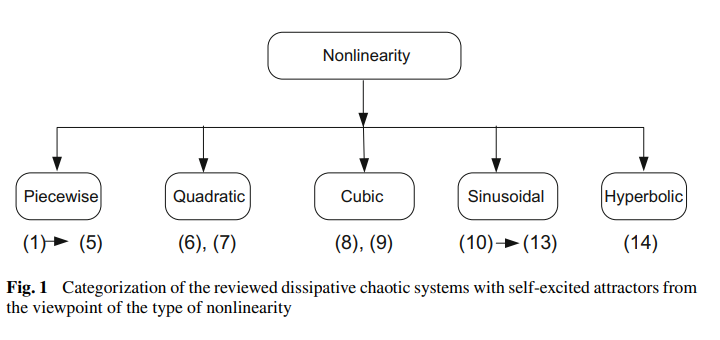
Chaos theory has attracted the interest of the scientific community because of its broad range of applications, such as in secure communications, cryptography or modeling multi-disciplinary phenomena. Continuous flows, which are expressed in terms of ordinary differential equations, can have numerous types of post transient solutions. Reporting when these systems of differential equations exhibit chaos represents a rich research field. A self-excited chaotic attractor can be detected through a numerical method in which a trajectory starting from a point on the unstable manifold in the neighborhood of an unstable equilibrium reaches an attractor and identifies it. Several simple systems based on jerk-equations and different types of nonlinearities were proposed in the literature. Mathematical analyses of equilibrium points and their stability were provided, as well as electrical circuit implementations of the proposed systems. The purpose of this chapter is double-fold. First, a survey of several self-excited dissipative chaotic attractors based on jerk-equations is provided. The main categories of the included systems are explained from the viewpoint of nonlinearity type and their properties are summarized. Second, maximum Lyapunov exponent values are explored versus the different parameters to identify the presence of chaos in some ranges of the parameters. © 2018, Springer International Publishing AG.