This paper introduces a study to generalize the design of a continuous time filters into the fractional order domain. The study involves inverting and non-inverting filters based on CFOA where three responses are extracted which are high-pass, band-pass and low-pass responses. The proposed study introduces the generalized formulas for the transfer function of each response with different fractional orders. The fractional-order filters enhance the design flexibility and controllability due to the extra degree of freedom provided by the fractional order parameters. The general fundamentals of

In this paper, a generalized fractional-order form of the simulated inductor using a single current feedback operational amplifier (CFOA) and a fractional-order capacitor is introduced. Analytical expression of the equivalent fractionalorder inductor versus the circuit elements is achieved. Moreover, the effect of the parasitic impedance and the non-idealities of the CFOA are investigated analytically with numerical simulations and circuit equivalent. Circuit simulations are discussed using AD844 spice model to validate the theoretical study of the fractional-order inductor. Simulations show

In this paper, a general analysis of the generation for all possible fractional order oscillators based on two-port network is presented. Three different two-port network classifications are used with three external single impedances, where two are fractional order capacitors and a resistor. Three possible impedance combinations for each classification are investigated, which give nine possible oscillators. The characteristic equation, oscillation frequency and condition for each presented topology are derived in terms of the transmission matrix elements and the fractional order parameters α

This paper presents a generalization of well-known phase shift oscillator based on single CCII into the fractional order domain. The general state matrix, characteristic equation and design equations are presented. The general oscillation frequency, condition and the phase difference between the oscillatory outputs are introduced in terms of the fractional order parameters. These parameters add extra degrees of freedom which in turn increase the design flexibility and controllability. Numerical discussion of five special cases is investigated including the integer case. Spice simulations and

This paper proposes a hardware platform implementation on FPGA for two fractional-order derivative operators. The Grünwald-Letnikov and Caputo definitions are realized for different fractional orders. The realization is based on non-uniform segmentation algorithm with a variable lookup table. A generic implementation for Grünwald-Letnikov is proposed and a 32 bit Fixed Point Booth multiplier radix-4 is used for Caputo implementation. Carry look-ahead adder, multi-operand adder and booth multiplier are used to improve the performance and other techniques for area and delay minimization have

This paper presents a generalization of Soliman's four-phase oscillator into the fractional-order domain. The extra degrees of freedom provided by the fractional-order parameters α and β add more flexibility to the design of the circuit. The design procedure and equations of the proposed oscillator are presented and verified using Matlab and PSPICE. Also, the stability analysis for fractional order systems is studied for different cases of α and β. © 2017 IEEE.

Fractional-order calculus is the branch of mathematics which deals with non-integerorder differentiation and integration. Fractional calculus has recently found its way to engineering applications; particularly electronic circuits with promising results showing the feasibility of fabricating fractional-order capacitors on silicon. Fractionalorder capacitors are lossy non-deal capacitors with an impedance given by Zc = (1/jωC)α, where C is the pseudo-capacitance and α is its order (0

This paper presents a general procedure to obtain Butterworth filter specifications in the fractional-order domain where an infinite number of relationships could be obtained due to the extra independent fractional-order parameters which increase the filter degrees-of-freedom. The necessary and sufficient condition for achieving fractional-order Butterworth filter with a specific cutoff frequency is derived as a function of the orders in addition to the transfer function parameters. The effect of equal-orders on the filter bandwidth is discussed showing how the integer-order case is considered

This paper introduces new meta-heuristic optimization algorithms for extracting the parameters of the Cole-impedance model. It is one of the most important models providing best fitting with the measured data. The proposed algorithms inspired by nature are known as Flower Pollination Algorithm (FPA) and Moth-Flame Optimizer (MFO). The algorithms are tested over sets of both simulated and experimental data. The results are compared with other fitting algorithms such as the Non-linear least square (NLS) and Bacterial Foraging Optimization (BFO). The comparison showed a better fit in the sum of

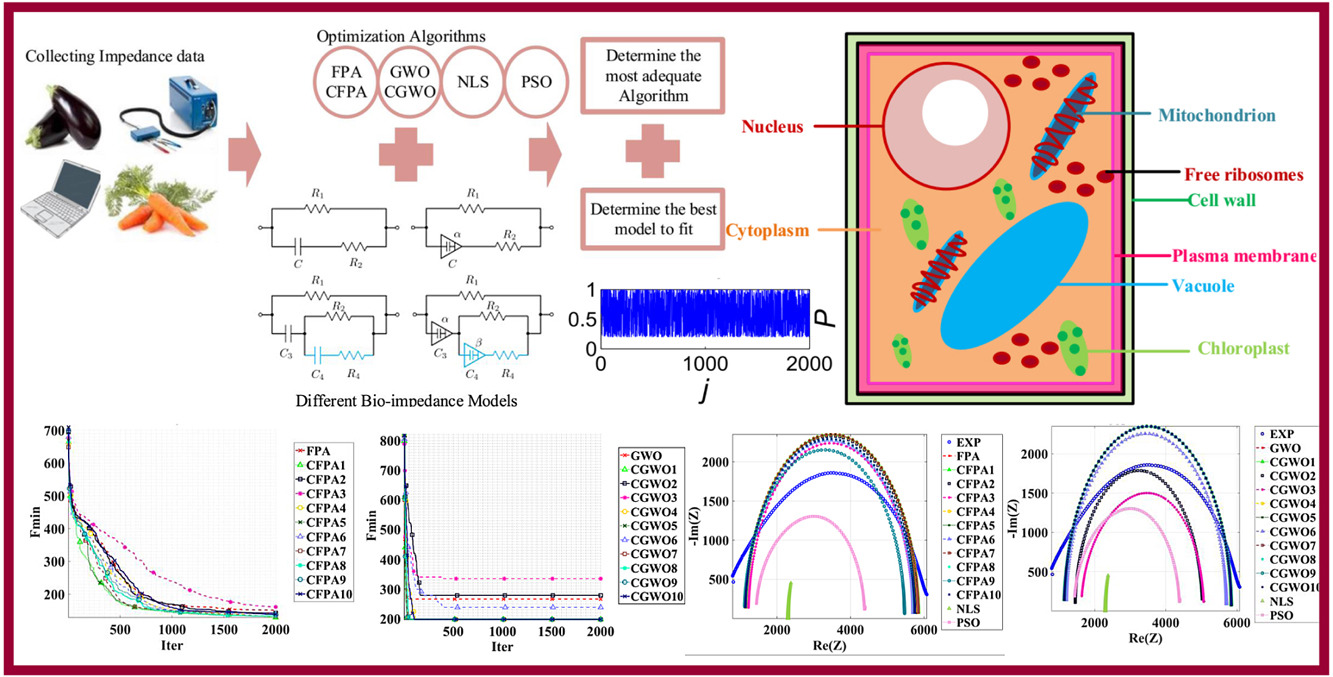
Precise parameter extraction of the bio-impedance models from the measured data is an important factor to evaluate the physiological changes of plant tissues. Traditional techniques employed in the literature for this problem are not robust which reflects on their accuracy. In this paper, the Flower Pollination Algorithm (FPA), the Grey Wolf Optimizer (GWO) and ten of their chaotic variants are employed to extract the parameters of bio-impedance models. These models are the simplified Hayden and Double-Shell models in their integer and fractional order forms. Experimental data sets of three