Recently, a new classification of nonlinear dynamics has been introduced by Leonov and Kuznetsov, in which two kinds of attractors are concentrated, i.e. self-excited and hidden ones. Self-excited attractor has a basin of attraction excited from unstable equilibria. So, from that point of view, most known systems, like Lorenz's system, Rössler's system, Chen's system, or Sprott's system, belong to chaotic systems with self-excited attractors. In contrast, a few unusual systems such as those with a line equilibrium, with stable equilibria, or without equilibrium, are classified into chaotic

Recently, a new classification of nonlinear dynamics has been introduced by Leonov and Kuznetsov, in which two kinds of attractors are concentrated, i.e. self-excited and hidden ones. Self-excited attractor has a basin of attraction excited from unstable equilibria. So, from that point of view, most known systems, like Lorenz’s system, Rössler’s system, Chen’s system, or Sprott’s system, belong to chaotic systems with self-excited attractors. In contrast, a few unusual systems such as those with a line equilibrium, with stable equilibria, or without equilibrium, are classified into chaotic

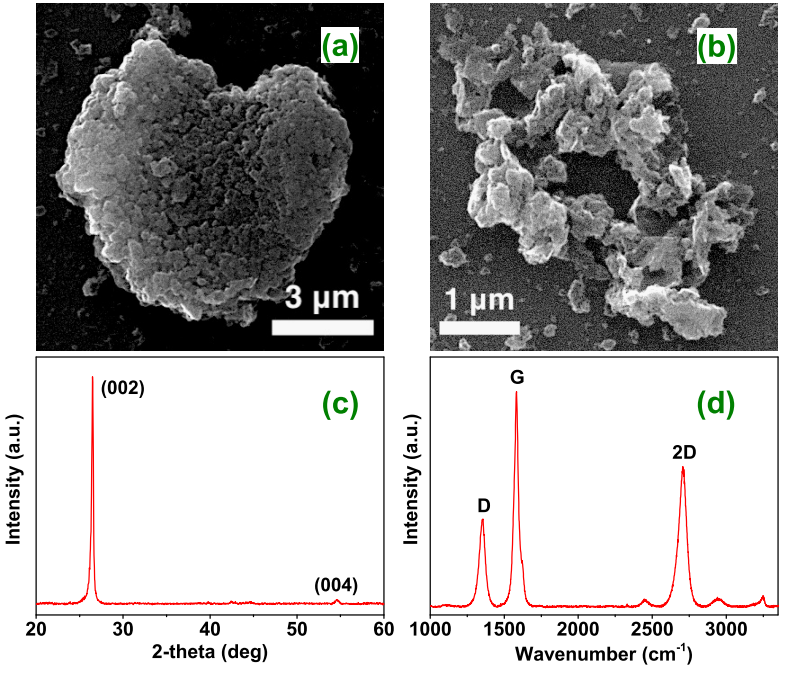
Supercapacitors are electrochemical devices that can store and restore electrical energy and are mostly used for powering dc or close-to-dc applications. As such they have not been explored enough for non-dc circuits. In this study, we implement a band-pass for frequency selectivity purposes and a relaxation oscillator for timing applications using a solid-state carbon electric double-layer capacitor. The expected behavior was observed for both circuits in the sub-Hertz and tens of Hertz frequency ranges. This confirms the possibility of using the frequency-dependent capacitive behavior of

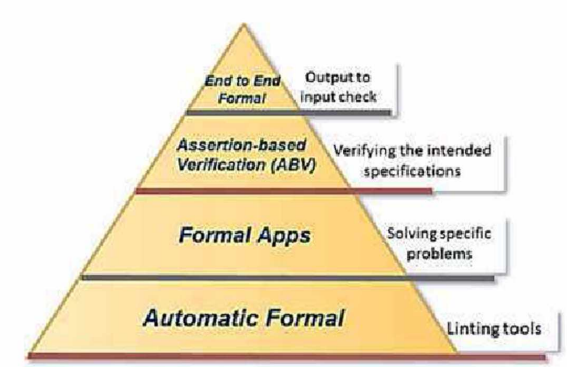
This paper posits an automatic handling to some of the most common RTL critical issues in the verification process. In this paper, we propose an automatic linting tool to handle some causes of intentional latches generated in the synthesis process and clock gating timing violation. Therefore, no need to waste verification time to dive through long codes to handle them manually. The proposed tool has been implemented using python to speed up the linting process with easy GUI. Finally, it has been tested on OpenCore certificated projects source codes. © 2018 IEEE.

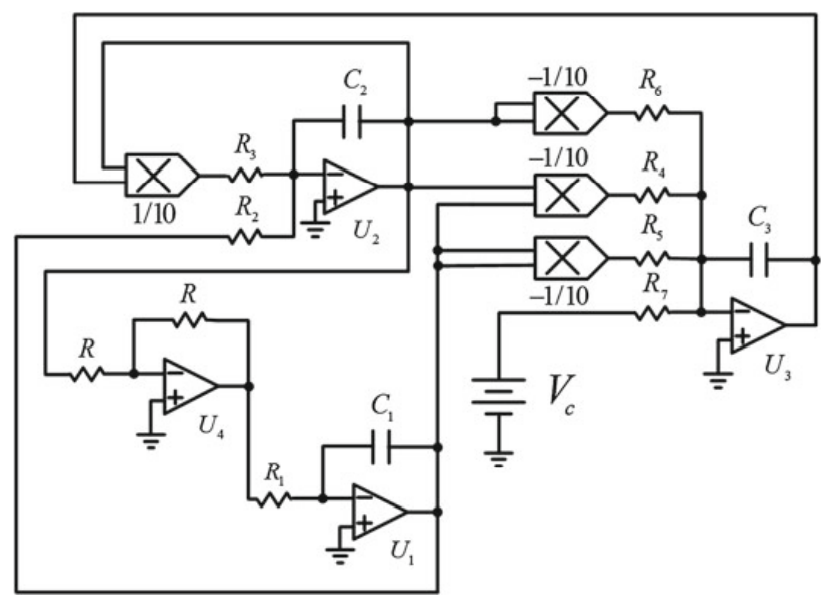
This paper proposes new multi-scrolls chaotic systems which is called the X-shape. The purpose is to have more complex systems and flexible ranges of the chaotic behavior. The proposed X-shape is a combination between V-shape and Λ-shape. This paper also represents the Heart-shape which considered a special case of the X-shape. The system complexity has been measured by MLE and compared with V-shape system. It shows lager MLE on the side of X-shape. In addition, the effect of changing system parameters has been discussed and compared with V-shape. Finally, a fully hardware implantation on FPGA

The promising capabilities of fractional-order devices challenge researchers to find a way to build it physically. Approximating the Laplacian operator sα can pave the way to emulate the fractional-order devices till its off-the-shelf appearance. This paper introduces three approximations of the Laplacian operator sα: Oustaloup, Matsuda, and Valsa by comparing their behaviors through two types of oscillator circuits. The first two are well-established approximations and the latter is proposed for the first time by converting its model network to an integer polynomial approximation of the

This paper introduces closed formulas of two topologies of fractional-order relaxation oscillators. One of these topologies is based on Operational Amplifier (Op-Amp) and the other one depends on Operational Operational Trans-Resistance Amplifier (OTRA). Special cases for each topology are also provided. The advantage of these designs comes from the added extra degree of freedom presented by the fractional-order α. Matsuda's approximation of sα is used to implement fractional-order capacitors. Also, experimental work is included to verify the theoretical results. © 2018 IEEE.

In this work, a novel implementation of a tunable fractional-order bandpass filter of order 2α is proposed. The transfer function of the presented filter is approximated using the second-order Continued Fraction Expansion (CFE) approximation technique. The filter transfer function is realized using the Inverse Follow the Leader Feedback (IFLF) structure. The Operational Transconductance Amplifiers (OTAs) are used to implement the filter circuit. Furthermore, the proposed filter is tunable by varying the value of only one bias current, which adjust the value of α. The simulations are performed

Recently, memristive oscillators are a significant topic in the nonlinear circuit theory where there is a possibility to build relaxation oscillators without existence of reactive elements. In this paper, a family of voltage-controlled memristor-based relaxation oscillator including two memristors is presented. The operation of two memristors-based voltage relaxation oscillator circuits is demonstrated theoretically with the mathematical analysis and with numerical simulations. The generalized expressions for the oscillation frequency and conditions are derived for different cases, where a

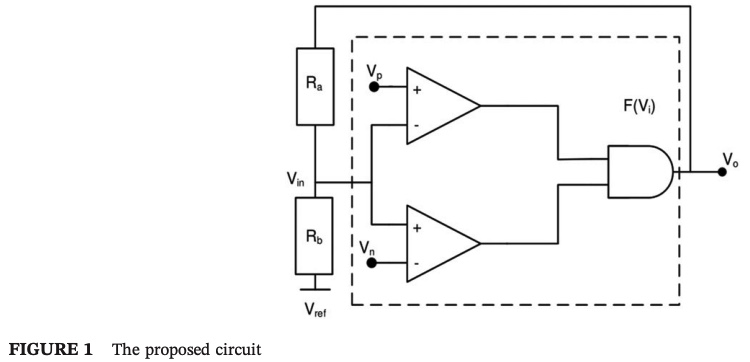
This paper demonstrates a low power 6-bit single-ended voltage-based Capacitance-to-Digital Converter (CDC) circuit based on a charge redistribution technique and Successive Approximation Register (SAR) logic operating at 370 kHz sampling rate. A proposed realization of a SAR logic control unit integrated with a low power comparator is introduced where the system blocks are entirely built on the transistor level. The system, which is fully automated with a universal clock signal, is tested for real time Cadence simulations using a 130nm model from which static and dynamic parameters are