A low-pass fractional-order filter topology based on a single metal oxide semiconductor transistor is presented in this Letter. The filter is realized using a fractional-order capacitor fabricated using multi-walled carbon nanotubes. The electronic tuning capability of the filter’s frequency characteristics is achieved through a biasing current source. Experimental results are presented and compared with the theory. © 2019, Springer Science+Business Media, LLC, part of Springer Nature.

Chebyshev filter is one of the most commonly used prototype filters that approximate the ideal magnitude response. In this paper, a simple and fast approach to create fractional order Chebyshev-like filter using its integer order poles is discussed. The transfer functions for the fractional filters are developed using the integer order poles from the traditional filter. This approach makes this work the first to generate fractional order transfer functions knowing their poles. The magnitude, phase, step responses, and group delay are simulated for different fractional orders showing their

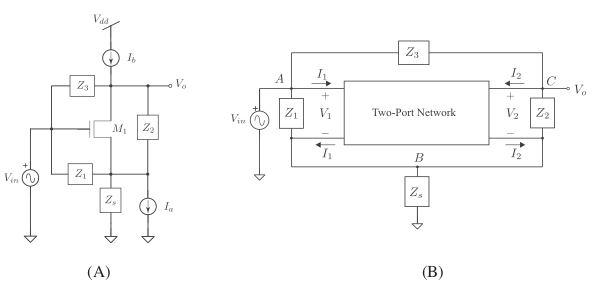
In this letter, all possible single transistor RC-only second-order allpass filters obtainable from a four impedance common-source topology are reported. It is shown that there are only seven such filters with only one of them being a minimum component canonical 2R-2C filter. Two of the found filters are designed and simulated in a 65-nm CMOS process. © 2019 John Wiley & Sons, Ltd.

This paper introduces the design procedure of the fractional-order Soliman Nonminimum-phase filter. Theoretical analysis has been carried out providing the critical frequencies of the filter. The effect of fractional-order parameter \alpha on the filter response has been investigated. Additionally, two different approximation techniques (Oustaloup and Matsuda) have been employed to realize the filter. A comparison is held between the exact and approximated solutions. Theoretical analysis is verified through circuit simulations and experimental work. © 2019 IEEE.

Modeling epidemiological dynamics of AIDS infection is an indispensable method to track the spread of such fatal disease. In this paper, the Differential Infectivity and Staged Progression Model, DISP, is modified to include the possibility of recovery, hence the new proposed model is called the DISPR model. The DISPR model is also generalized to the fractional order domain to allow more flexibility. In order to compare, both models are tested on the same sample of population. The DISPR model is proved to be valid by predicting the same behavior of the DISP model and real epidemiology

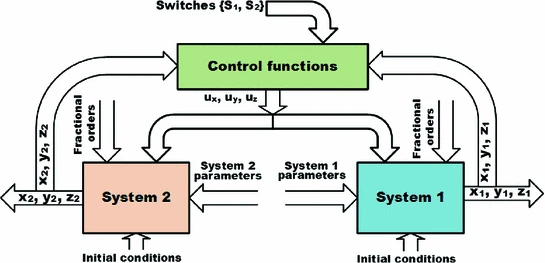
The chaotic dynamics of fractional-order systems and their applications in secure communication have gained the attention of many recent researches. Fractional-order systems provide extra degrees of freedom and control capability with integer-order differential equations as special cases. Synchronization is a necessary function in any communication system and is rather hard to be achieved for chaotic signals that are ideally aperiodic. This chapter provides a general scheme of control, switching and generalized synchronization of fractional-order chaotic systems. Several systems are used as

The chaotic dynamics of fractional-order systems and their applications in secure communication have gained the attention of many recent researches. Fractional-order systems provide extra degrees of freedom and control capability with integer-order differential equations as special cases. Synchronization is a necessary function in any communication system and is rather hard to be achieved for chaotic signals that are ideally aperiodic. This chapter provides a general scheme of control, switching and generalized synchronization of fractional-order chaotic systems. Several systems are used as

A novel double-bound hysteretic regulation scheme to control multi-phase interleaved Switched-Capacitor DC-DC converters is presented. The control scheme adjusts the number of interleaved phases with the SC converter's switching frequency to significantly reduce the required operating frequency of the control comparator, enabling the practical application of hysteretic control with large number of interleaved phases. A 16-phase 2:1 SC converter is designed in 65-nm TSMC low-power CMOS process using the proposed technique. The converter with the new hysteretic control achieves fast dynamic

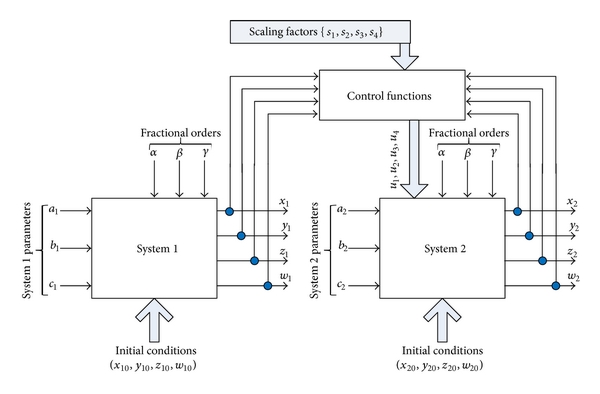
This paper presents a general synchronization technique and an amplitude modulation of chaotic generators. Conventional synchronization and antisynchronization are considered a very narrow subset from the proposed technique where the scale between the output response and the input response can be controlled via control functions and this scale may be either constant (positive, negative) or time dependent. The concept of the proposed technique is based on the nonlinear control theory and Lyapunov stability theory. The nonlinear controller is designed to ensure the stability and convergence of

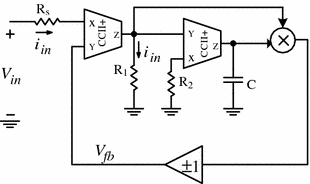
This chapter introduces different generalized mathematical classes of memristors which can be categorized as: continuous symmetrical models (current and voltage controlled emulators), continuous nonsymmetrical model, switched-memristor model, and fractional-order model with some experimental results. Different emulators with experimental results are discussed based on CCII, discrete components, and MOS realizations. Different analytical expressions, numerical analyses, circuit simulations results as well as experimental results are provided for most of the previous models. © 2015, Springer