
Circuit Theory and Applications
A novel artificial intelligent-based approach for real time prediction of telecom customer’s coming interaction
Predicting customer’s behavior is one of the great challenges and obstacles for business nowadays. Companies take advantage of identifying these future behaviors to optimize business outcomes and create more powerful marketing strategies. This work presents a novel real-time framework that can predict the customer’s next interaction and the time of that interaction (when that interaction takes place). Furthermore, an extensive data exploratory analysis is performed to gain more insights from the data to identify the important features. Transactional data and static profile data are integrated
A Novel Deep-learning based Approach for Automatic Diacritization of Arabic Poems using Sequence-to-Sequence Model
Over the last 10 years, Arabic language have attracted researchers in the area of Natural Language Processing (NLP). A lot of research papers suddenly emerged in which the main work was the processing of Arabic language and its dialects too. Arabic language processing has been given a special name ANLP (Arabic Natural Language Processing). A lot of ANLP work can be found in literature including almost all NLP applications. Many researchers have been attracted also to Arabic linguistic knowledge. The work expands from Basic Language Analysis to Semantic Level Analysis. But Arabic text semantic
Automatic Detection of Alzheimer Disease from 3D MRI Images using Deep CNNs
Alzheimer's disease (AD), also referred to simply as Alzheimer's, is a chronic neurodegenerative disease that usually starts slowly and worsens over time. It is the cause of 60% to 70% of cases of dementia. In 2015, there were approximately 29.8 million people worldwide with AD. It most often begins in people over 65 years of age as it affects about 6% of people 65 years and older, although 4% to 5% of cases are early-onset Alzheimer's which begin before this. In 2015, researchers have figured out that dementia resulted in about 1.9 million deaths. Continuous efforts are made to cure the
Multiobjective design optimization of parabolic trough collectors
Despite the large amount of research conducted on PTC performance analysis, few and rare numbers of research have considered the design optimization of PTCs. In the present work, a novel multiobjective-optimization model is developed for design optimization of PTCs. The objective functions are the thermal and exergetic efficiencies because they are the most important performance indicators (PIs) of PTCs. The design variables are the inlet temperature, and the outlet and inlet diameters of the PTC receiver tube. The PTC material volume (refers to the volume of the PTC receiver and collector) is
Analysis, control, and optimization of aeroelastic systems: An introduction to the recent literature for the new investigator
Aeroelasticity studies the static and dynamic interaction between structural deformation and fluid forces. As a result, the aeroelasticity is usually divided into three parts: aerodynamics, structural response, and dynamics with statics as a special case. Instabilities may occur to this interaction (feedback) that lead to structural failure and, even when no instability occurs, the interaction may lead to degradation or improvement of the system performance. There are several unstable phenomena may occur for elastic bodies such as flutter, divergence, low cycle oscillation, buffet, and control
Specialized Syntactic Quran Search Engines: Evaluation and Limitations
The Quran is the sacred text that provides guidance and teachings to the followers of Islam. This paper aims to analyze and evaluate the limitations of current specialized search engines used for retrieving information from the Quran. Also, this work includes an initial evaluation of Quran search with a large language model (LLM) employing prompt engineering. The study focuses on the syntactic aspect of information retrieval, while acknowledging the necessity of considering the semantic meaning of Quranic words and verses for a more comprehensive analysis. Furthermore, recommendations and

Improving the Performance of Semantic Text Similarity Tasks on Short Text Pairs
Training semantic similarity model to detect duplicate text pairs is a challenging task as almost all of datasets are imbalanced, by data nature positive samples are fewer than negative samples, this issue can easily lead to model bias. Using traditional pairwise loss functions like pairwise binary cross entropy or Contrastive loss on imbalanced data may lead to model bias, however triplet loss showed improved performance compared to other loss functions. In triplet loss-based models data is fed to the model as follow: Anchor sentence, positive sentence and negative sentence. The original data
Using Knowledge Graph Embeddings in Embedding Based Recommender Systems
This paper proposes using entity2rec [1] which utilizes knowledge graph-based embeddings (node2vec) instead of traditional embedding layers in embedding based recommender systems. This opens the door to increasing the accuracy of some of the most implemented recommender systems running in production in many companies by just replacing the traditional embedding layer with node2vec graph embedding without the risk of completely migrating to newer SOTA systems and risking unexpected performance issues. Also, Graph embeddings will be able to incorporate user and item features which can help in
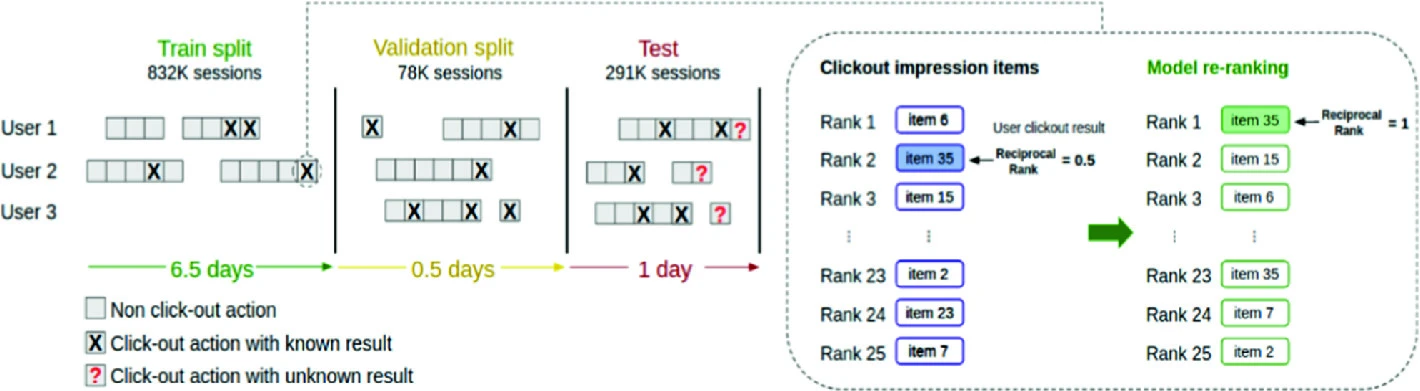
Recommendations on Streaming Data: E-Tourism Event Stream Processing Recommender System
The Association for Computing Machinery ACM recommendation systems challenge (ACM RecSys) [1] released an e-tourism dataset for the first time in 2019. Challenge shared hotel booking sessions from trivago website asking to rank the hotels list for the users. Better ranking should achieve higher click out rate. In this context, Trivago dataset is very important for e-tourism recommendation systems domain research and industry as well. In this paper, description for dataset characteristics and proposal for a session-based recommender system in addition to a comparison of several baseline

Dynamic Modeling and Identification of the COVID-19 Stochastic Dispersion
In this work, the stochastic dispersion of novel coronavirus disease 2019 (COVID-19) at the borders between France and Italy has been considered using a multi-input multi-output stochastic model. The physical effects of wind, temperature and altitude have been investigated as these factors and physical relationships are stochastic in nature. Stochastic terms have also been included to take into account the turbulence effect, and the r and om nature of the above physical parameters considered. Then, a method is proposed to identify the developed model's order and parameters. The actual data has