Plasmonic Photovoltaics are considered as a promising candidate for enhancing the optical absorption by embedding metallic nanoparticles that confine the incident light in the cell. This results in thin-film PVs with improved efficiency. In this paper, the effects of embedding both conical and cylindrical metal nanoparticles in plasmonic PVs are investigated. The extinction cross sections for these designs are calculated. The improvement of the optical absorption of the solar cell due to these nanoparticles is proved and compared. Finally, the effects of the design parameters of these

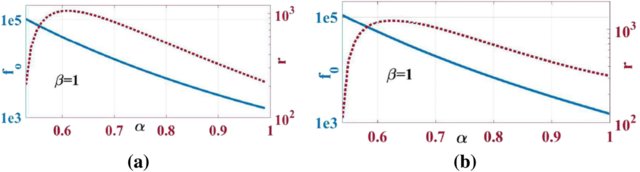
This paper presents a study for general fractional order oscillator based on two port network where two topologies of oscillator structure with two impedances are discussed. The two impedances are chosen to be fractional elements which give four combinations for each topology. The general oscillation frequency, condition and the phase difference between the two oscillatory outputs are deduced in terms of the transmission matrix parameter of a general two port network. As a case study: two different networks are presented which are op-amp based circuit and non-ideal gyrator circuit. The

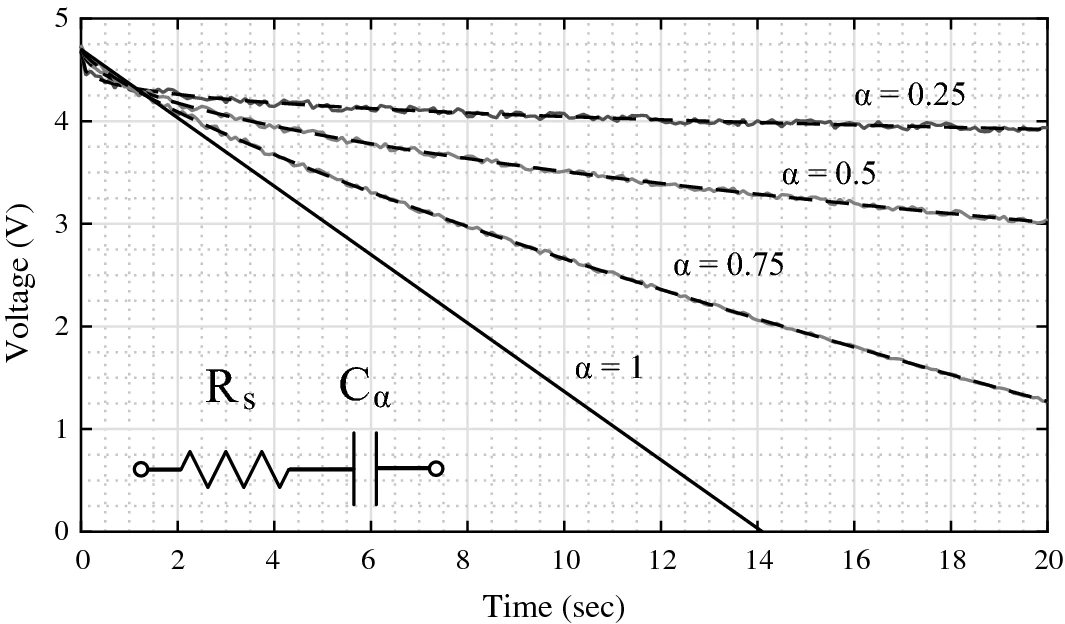
Optimization routines are widely used to numerically determine a set of model parameters that best fit collected experimental data. One recent application of these methods is to extract the fractional-order circuit model parameters that accurately characterize the transient behavior of discharging supercapacitors. However, the variability that these methods introduce to the extracted model parameters must be understood to determine if changes in model parameters are artifacts of the optimization routine or are representative of physical changes in the device under study. In this work, the

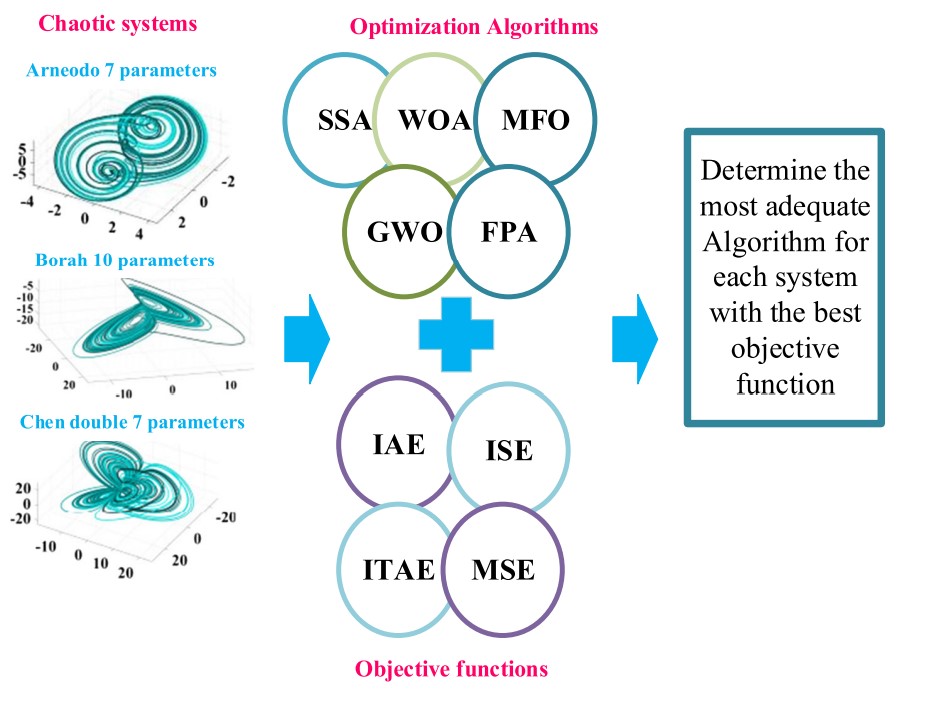
Fractional-order chaotic systems (FOCS) parameter identification is an essential issue in chaos control and synchronization process. In this paper, different recent Meta-heuristic Optimization Algorithms are used to estimate the parameters and orders of three FOCS. The investigated systems are Arneodo, Borah rotational attractor and Chen double- and four-wing systems. The employed algorithms are the Salp Swarm Algorithm, Whale Optimization Algorithm, Moth-Flame Optimizer, Grey Wolf Optimizer and the Flower Pollination Algorithm (FPA). The proposed algorithms are applied on several objective

This paper studies the famous Fitzhugh-Nagumo and Izhikevich neuron models in the fractional-order domain. Generalization of the integer models into the fractional-order domain providing a wider scope understanding of the neuron systems. The fractional Fitzhugh-Nagumo circuit model and the state space equations are introduced. Different fractional orders are studied as an example. Numerical solutions of the systems are given using non-standard finite difference scheme together with Grunwald-Letnikov discretization technique which is computationally efficient and accurate. The two models are

For the specifications of Wireless Body Area Networks (WBANs), eHealth systems, and wearable devices, batteries are not desirable. They maximize the sensor nodes’ size and need to be replaced every few years through human interference. Energy harvesting is now being studied as the primary source of electricity for wearable devices. Several initiatives have succeeded in using energy harvesting to operate the wearable devices’ electronic components. However, to rely primarily on energy harvesting in wearable devices, some obstacles need to be addressed. This work surveys the development of

Interconnect design has recently become one of the important factors that affect the circuit delay and performance especially in the deep submicron technology. The modelling of interconnects is typically based on using Elmore definitions of the delay time and rise time. So, a general formula for Elmore delay time and rise time in the fractional order domain are presented in this work. It is found from the new formulas of the delay time and rise time that these timing values could be controlled or tuned by the fractional orders. Hence, the fractional order can compensate for the components

The fractional-order model of a phantom electroencephalographic system, at various distances between electrodes, is realized using appropriate decomposition of the rational transfer functions which approximate the highpass filters that describe its dynamics. The main offered benefits, in comparison to the corresponding straightforward implementations of the rational transfer functions, are the capability of monolithic implementation due the minimization of the maximum value of the required capacitances and, also, the reduced power consumption. The performance of the presented filter topologies

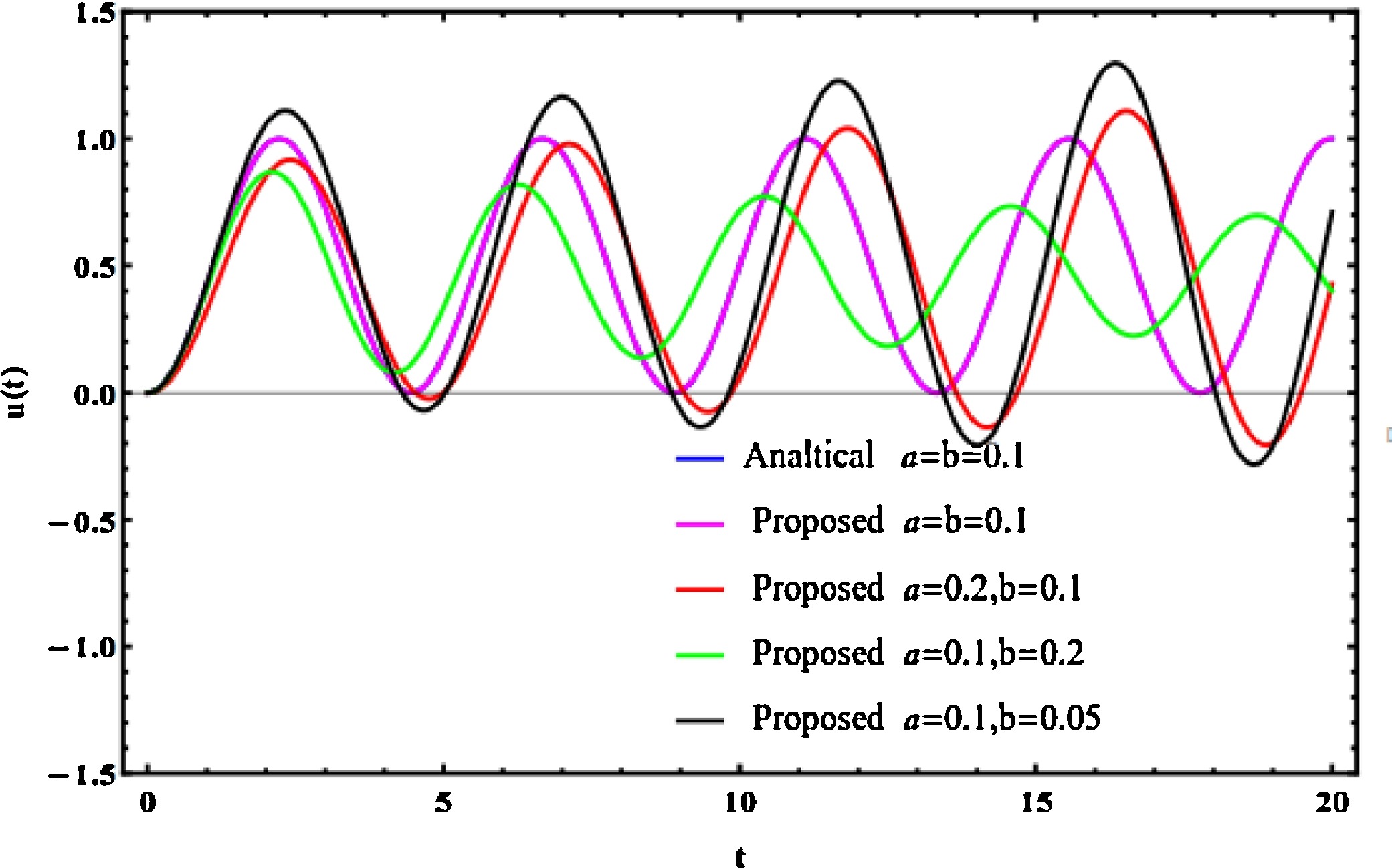
This paper introduces two methods for the numerical solution of distributed order linear fractional differential equations. The first method focuses on initial value problems (IVPs) and based on the αth Caputo fractional definition with the shifted Chebyshev operational matrix of fractional integration. By applying this method, the IVPs are converted into simple linear differential equations which can be easily handled. The other method focuses on boundary value problems (BVPs) based on Picard's method frame. This method is based on iterative formula contains an auxiliary parameter which

Red phosphorus and sulfurized polyacrylonitrile (RP-SPAN) composite has recently shown promising results as an anode material in lithium-ion battery applications. However, the stability analysis of its dynamic response has not been investigated yet. In this study we use the transfer function stability analysis, the Kramers-Kronig (KK) integral relations, and the differential capacity analysis to evaluate the cell's behavior in both frequency and time domains in terms of stationarity, stability, linearity, as well as dissipation and degradation with extended charge/discharge cycling. The