
Circuit Theory and Applications
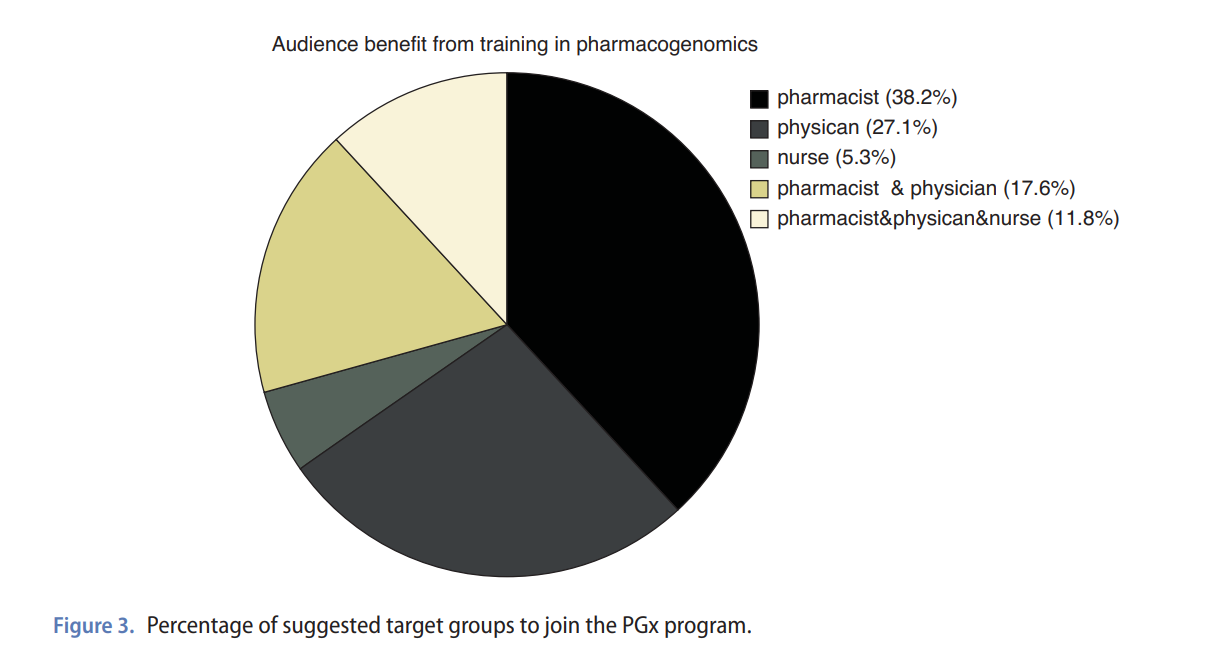
Analysis of the current situation of pharmacogenomics in terms of educational and healthcare needs in Egypt and Lebanon
Pharmacogenomics (PGx) is a practice that investigates the link between genetic differences and drug response in patients. This can improve treatment effectiveness and reduce harmful side effects. However, has yet to be adequately realized in developing nations. Three surveys were conducted between November 2022 to March 2023 in Egypt and Lebanon. The first survey assessed availability of PGx testing in different healthcare facilities; the second one assessed knowledge, interest and attitude toward learning about PGx among pharmacists and physicians; and the third one assessed interest in
The Melody of Silent Mutations: Microbiome Adaptation Across the Subduction Zone
Silent mutations generate synonymous codons that encode the same amino acid however, they may be silent yet operative. These synonymous codons are used in unequal frequencies resulting in a phenomenon known as codon usage bias (CUB). It drives gene expression towards highly expressed and adaptation genes. In this study we investigated CUB in one of the largest, most dynamic exotic niches, the volcanic subduction zones in Costa Rica. CUB analysis in such challengingly inaccessible sites can help distinguish highly expressed genes under certain environmental factors, elucidating molecular
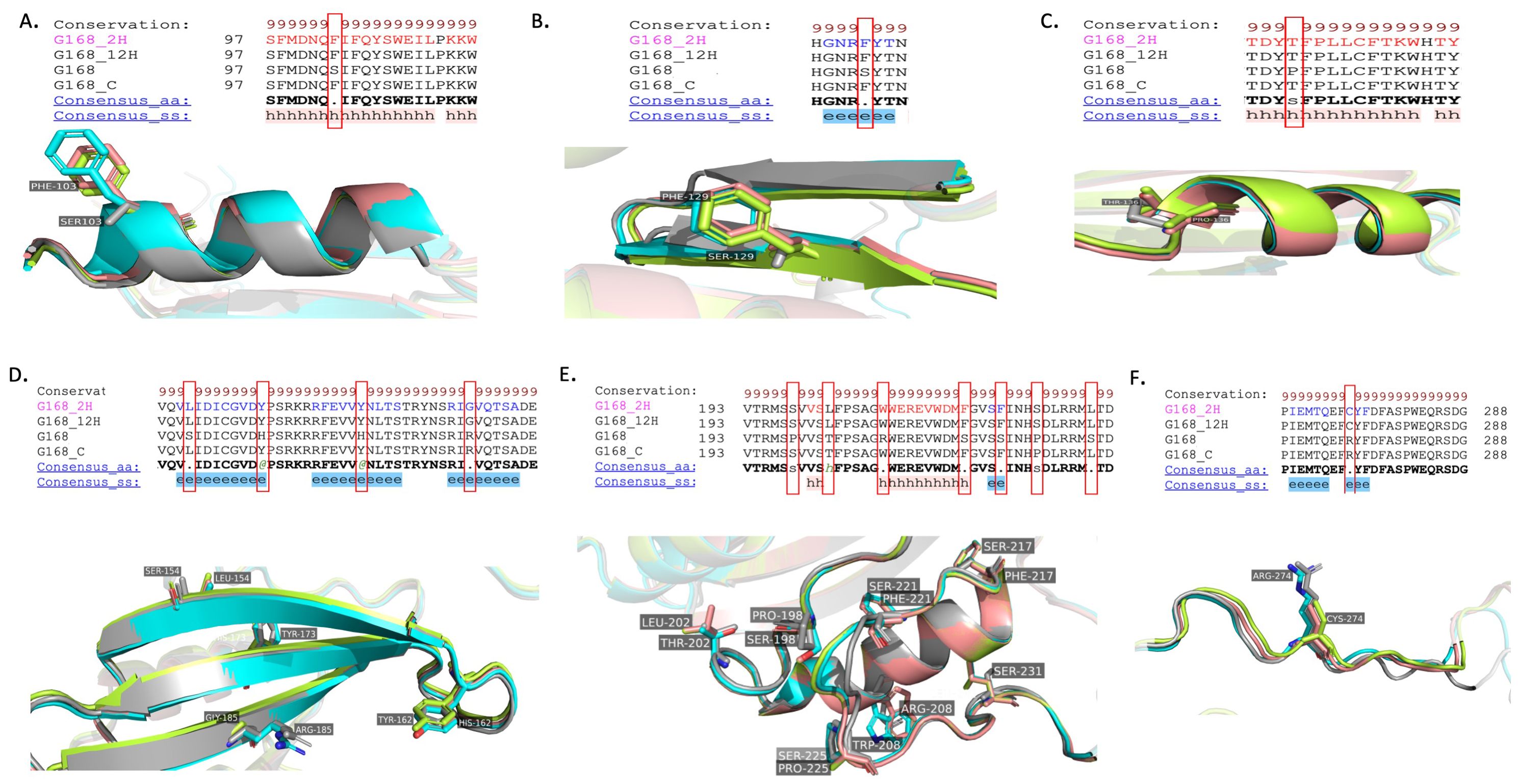
RNA editing-induced structural and functional adaptations of NAD9 in Triticum aestivum under drought stress
Introduction: Mitochondria are essential organelles in eukaryotic cells, producing ATP through the electron transport chain to supply energy for cellular activities. Beyond energy production, mitochondria play crucial roles in cellular signaling, stress responses, and the regulation of reactive oxygen species. In plants, mitochondria are one of the keys to responding to environmental stresses which can significantly affect crop productivity, particularly in crops like wheat. RNA editing, a post-transcriptional RNA modification process in mitochondria, is linked to regulating these stress
Chronic tobacco smoking and neurocognitive impairments in adolescents and young adults: a systematic review and meta-analysis
There is a lack of robust research investigating the association between neurocognitive impairments and chronic tobacco smoking in adolescents/young adults. Therefore, a systematic review and meta-analysis were conducted to examine this association by pooling cross-sectional studies published from 1980 to 2023. The systematic review assessed the neurocognitive performances between chronic tobacco smokers and non-smokers in each study. The meta-analysis included six studies that compared chronic tobacco smokers against non-smokers using neuropsychological tests covering three neurocognitive
Identification and expression analysis of SBP-Box-like (SPL) gene family disclose their contribution to abiotic stress and flower budding in pigeon pea (Cajanus cajan)
The SPL gene family (for Squamosa Promoter-binding like Proteins) represents specific transcription factors that have significant roles in abiotic stress tolerance, development and the growth processes of different plants, including initiation of the leaf, branching and development of shoot and fruits. The SPL gene family has been studied in different plant species; however, its role is not yet fully explored in pigeon pea (Cajanus cajan). In the present study, 11 members of the CcSPL gene family were identified in C. cajan. The identified SPLs were classified into nine groups based on a
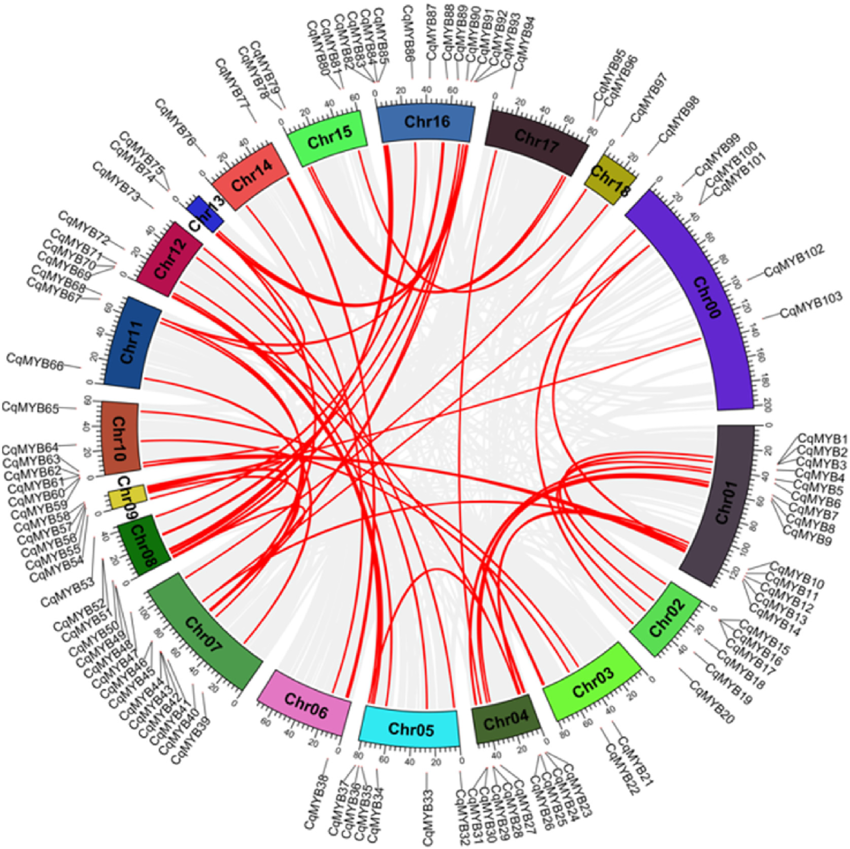
Genome-wide identification, phylogeny and expression analysis of the R2R3-MYB gene family in quinoa (Chenopodium quinoa) under abiotic stress
The MYB transcription factor (TF) are among the largest gene families of plants being responsible for several biological processes. The R2R3-MYB gene family are integral player regulating plant primary and secondary metabolism, growth and development, and responses to hormones and stresses. The phylogenetic analysis combined with gene structure analysis and motif determination resulted in division of R2R3-MYB gene family into 27 subgroups. Evidence generated from synteny analyses indicated that CqR2R3-MYBs gene family is featured by tandem and segmental duplication events. On the basis of RNA
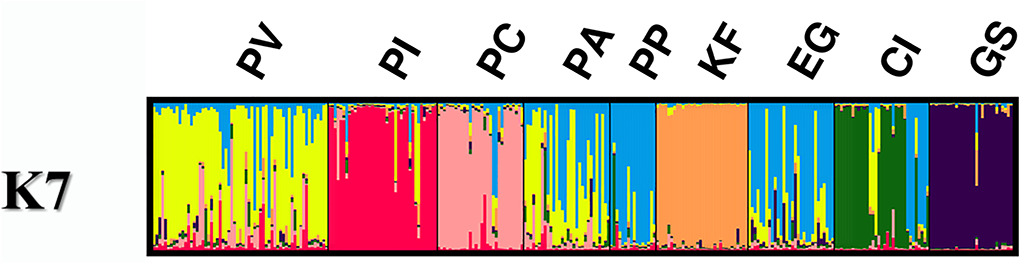
Phylogeographic and population genetic structure of hound-like native dogs of the Mediterranean Basin
The dog was probably the first domesticated animal. Despite extensive archaeological and genetic investigations, the origin and the evolution of the extant dogs are still being debated. Dog breeds that have over time been selected for hunting share common ancestral traits. This study represents the first comprehensive attempt to survey at the genomic and mitochondrial level eight hound-like dogs breeds indigenous to the Mediterranean Basin to determine if they share common ancient origins. Results from the microsatellite analysis indicate that all the dog populations have a low inbreeding
Morphogenetic characterization of Stenotrophomonas maltophilia infecting white stripe disease of rice (Oryza sativa L.)
Rice is a major cereal crop which ensure food security to more than half of the global population. Several biotic factors impact rice grain quality and its final production. White stripe disease, caused by pathogen Stenotrophomonas maltophilia is considered among the major limiting factor for reducing rice yields and quality. Present study was performed to understand the white stripe disease, which has been frequently misdiagnosed as bacterial leaf blight (BLB) due to similar symptoms. A survey was carried out based on accessibility and farmer participation to monitor incidence and sample
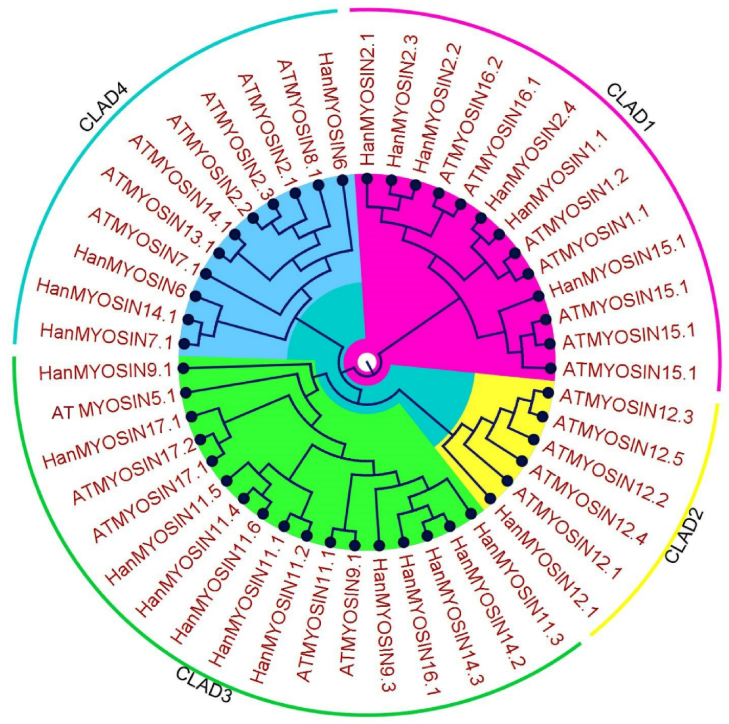
Genome-wide comparison and identification of myosin gene family in Arabidopsis thaliana and Helianthus annuus
Myosins are essential components of organelle trafficking in all the eukaryotic cells. Myosin driven movement plays a vital role in the development of pollen tubes, root hairs and root tips of flowering plants. The present research characterized the myosin genes in Arabidopsis thaliana and Helianthus annuus by using different computational tools. We discovered a total of 50 myosin genes and their splice variants in both pant species. Phylogenetic analysis indicated that myosin genes were divided into four subclasses. Chromosomal location revealed that myosin genes were located on all five
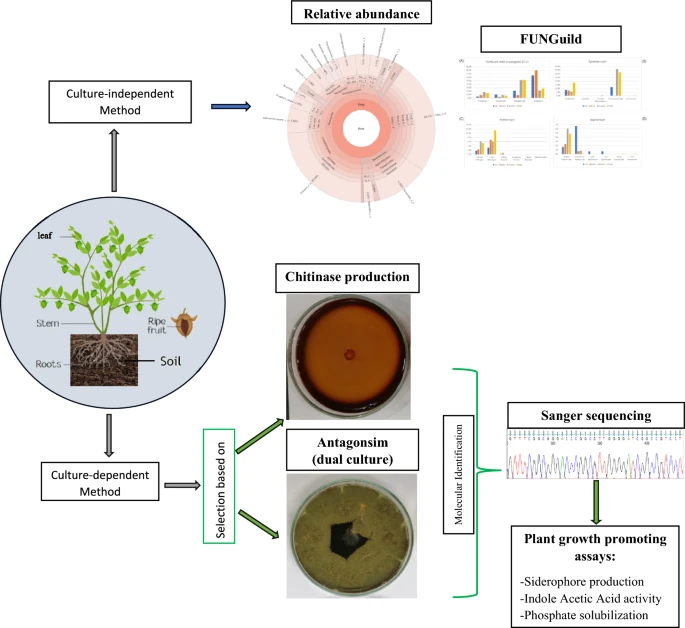
Revealing the diversity of Jojoba-associated fungi using amplicon metagenome approach and assessing the in vitro biocontrol activity of its cultivable community
Jojoba shrubs are wild plants cultivated in arid and semiarid lands and characterized by tolerance to drought, salinity, and high temperatures. Fungi associated with such plants may be attributed to the tolerance of host plants against biotic stress in addition to the promotion of plant growth. Previous studies showed the importance of jojoba as jojoba oil in the agricultural field; however, no prior study discussed the role of jojoba-associated fungi (JAF) in reflecting plant health and the possibility of using JAF in biocontrol. Here, the culture-independent and culture-dependent approaches