
Circuit Theory and Applications

Bio-inspired adsorption sheets from waste material for anionic methyl orange dye removal
Abstract: Nano zero-valent iron (nZVI), bimetallic nano zero-valent iron-copper (Fe0–Cu), and Raw algae (sargassum dentifolium) activated carbon-supported bimetallic nano zero-valent iron-copper (AC-Fe0–Cu) are synthesized and characterized using FT-IR, XRD, and SEM. The maximum removal capacity is demonstrated by bimetallic activated carbon AC-Fe0–Cu, which is estimated at 946.5 mg/g capacity at the condition pH = 7, 30 min contact time under shaking at 120 rpm at ambient temperature, 200 ppm of M.O, and 1 g/l dose of raw algae-Fe0–Cu adsorbent. The elimination capability of the H3PO4
Valorization of Agricultural and Marine Waste for Fabrication of Bio-Adsorbent Sheets
Industrial wastewater often contains considerable amounts of toxic pollutants that would endanger public health and the environment. In developing countries, these toxins are often discharged into natural ecosystems without pretreatment as it requires costly treatment processes, which causes long-term harmful socioeconomic impacts. Employing wastewater treatment plants using physical, biological, and chemical methods to clean the wastewater is considered by many nations the answer to the environmental crises. The treated water could be used for targeting the irrigation systems in its majority
Voltage-controlled M-M relaxation Oscillator
This paper discusses voltage-controlled M-M relaxation oscillator with analytical and circuit simulations. The introduced circuit has two different configurations based on the polarities of memristor; whether they are in the same direction or in the opposite direction. The Analytical formulas are function of the reference voltage such as the oscillation frequency and oscillation conditions for each case are derived with some numerical examples. The circuit simulations are introduced to validate the mathematical concepts as well as the effect of the reference voltage which can be used in

Fractional-order oscillators based on a single Op-Amp
This chapter introduces a family of fractional-order oscillators based on a single operational amplifier (Op-Amp) with two fractional-order capacitors. Twelve different fractional-order oscillator circuits are investigated where the state matrix, oscillation frequency, and oscillation condition for each circuit are presented. The phase difference between the two oscillatory outputs is deduced in terms of the fractional-order parameters. The fractional-order parameter enhances the oscillator performance by providing an extra degree-of-freedom. Also, the resulting circuits provide independent
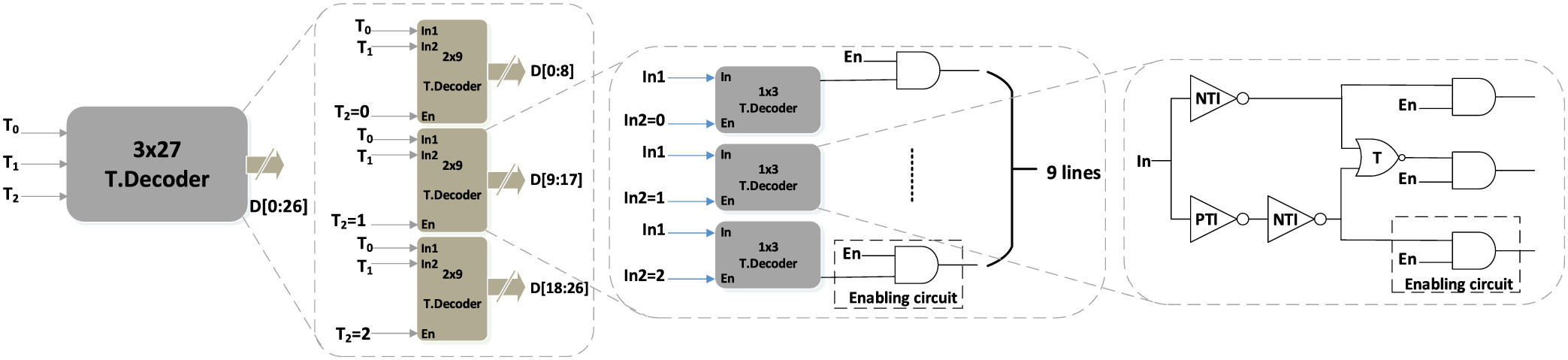
CNTFET-based ternary address decoder design
With the end of Moore's law, new paradigms are investigated for more scalable computing systems. One of the promising directions is to examine the data representation toward higher data density per hardware element. Multiple valued logic (MVL) emerged as a promising system due to its advantages over binary data representation. MVL offers higher information processing within the same number of digits when compared with binary systems. Accessing memory is considered one of the most power- and time-consuming instructions within a microprocessor. In the quest for building an entire ternary

CNTFET-based Approximate Ternary Adder Design
Multiple-Valued Logic (MVL) offers better data representation allowing higher information processing within the same amount of digits. With a trade-off in accuracy, approximate computation is a method to improve the power, size, and speed of digital circuits. This paper presents the design of CNTFET-based ternary half adder, full adder, 2-trit carry ripple adder, and 4trit carry ripple adder with different accuracies. The proposed designs are implemented using HSPICE tool and simulated for power consumption, delay, and error analysis. The trade-off between the transistor count and the
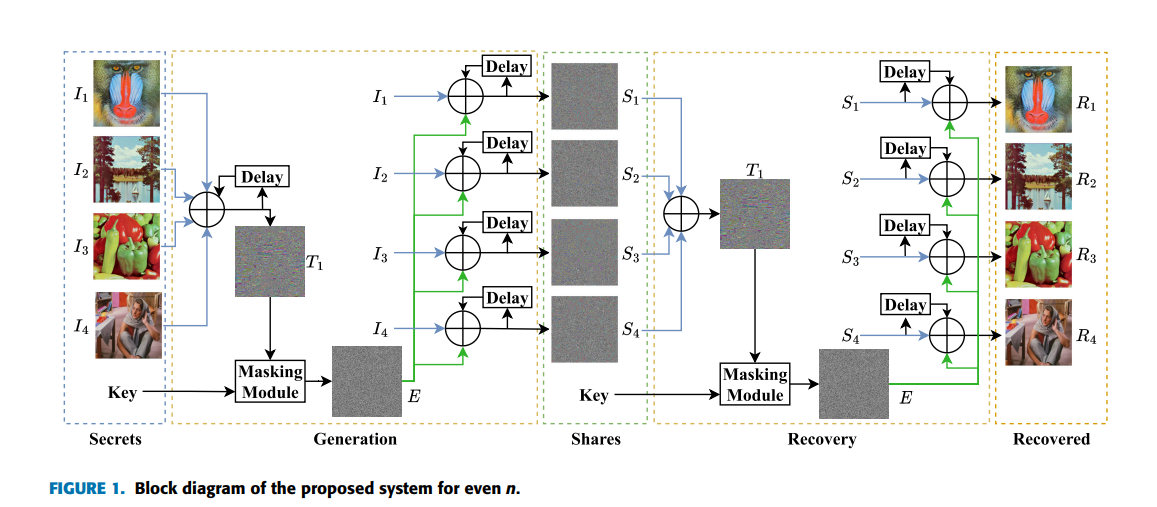
An Efficient Multi-Secret Image Sharing System Based on Chinese Remainder Theorem and Its FPGA Realization
Multi-Secret Image Sharing (MSIS) is important in information security when multiple images are shared in an unintelligible form to different participants, where the images can only be recovered using the shares from participants. This paper proposes a simple and efficient ( n,n )-MSIS system for colored images based on XOR and Chinese Remainder Theorem (CRT), where all the n share are required in the recovery. The system improves the security by adding dependency on the input images to be robust against differential attacks, and by using several delay units. It works with even and odd number
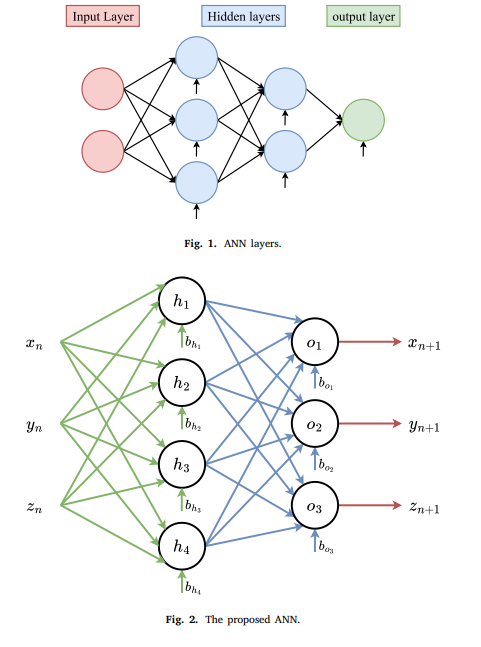
Artificial Neural Network Chaotic PRNG and simple encryption on FPGA
Artificial Neural Networks (ANNs) are remarkably able to fit complex functions, making them useful in various applications and systems. This paper uses ANN to fit the Pehlivan–Uyaroglu Chaotic System (PUCS) to produce an Artificial Neural Network Chaotic Pseudo-Random Number Generator (ANNC-PRNG). The proposed PRNG imitates the PUCS chaotic system's properties and attractor shape. The proposed ANNC-PRNG is implemented in a simple image encryption system on the Xilinx Kintex-7 Genesys 2 Field Programmable Gate Array (FPGA) board. Hardware realization of an ANN trained on chaotic time series has
A Secured Lossless Visual Secret Sharing for Color Images Using Arnold Transform
Nowadays, with the rapid growth in information, a fast and secure method is eagerly needed to share images. (n, n)-Visual Secret Sharing (VSS) is used to share a secret image into n shares, where the secret can only be recovered using all the n shares and the recovery must be fast with low computational complexity. This paper proposes a secured lossless (n, n)-VSS system based on Arnold transform and pixel vectorization suitable to be used with binary, grayscale and color images. Multiple security tests were performed such as entropy, correlation, Mean Squared Error (MSE), National Institute
A Unified System for Encryption and Multi-Secret Image Sharing Using S-box and CRT
Multi-Secret Image Sharing (MSIS) is used when multiple images need to be shared to multiple participants, but the images can not be recovered without the presence of all shares. In this paper, a unified system for performing encryption and (n,n)-MSIS is proposed. While MSIS is based on the XOR operation, encryption combines the utilization of Chinese Remainder Theorem (CRT), SHA-256, and S-box for improved security. The same designed system is used for the generation of secret shares and the recovery of secret images. In addition, a sensitive system key is designed where three pairwise