This article proposes a numerical solution approach and Field Programmable Gate Array implementation of a delayed fractional-order system. The proposed method is amenable to a sufficiently efficient hardware realization. The system's numerical solution and hardware realization have two requirements. First, the delay terms are implemented by employing LookUp Tables to keep the already required delayed samples in the dynamical equations. Second, the fractional derivative is numerically approximated using Grünwald-Letnikov approximation with a memory window size, L, according to the short memory

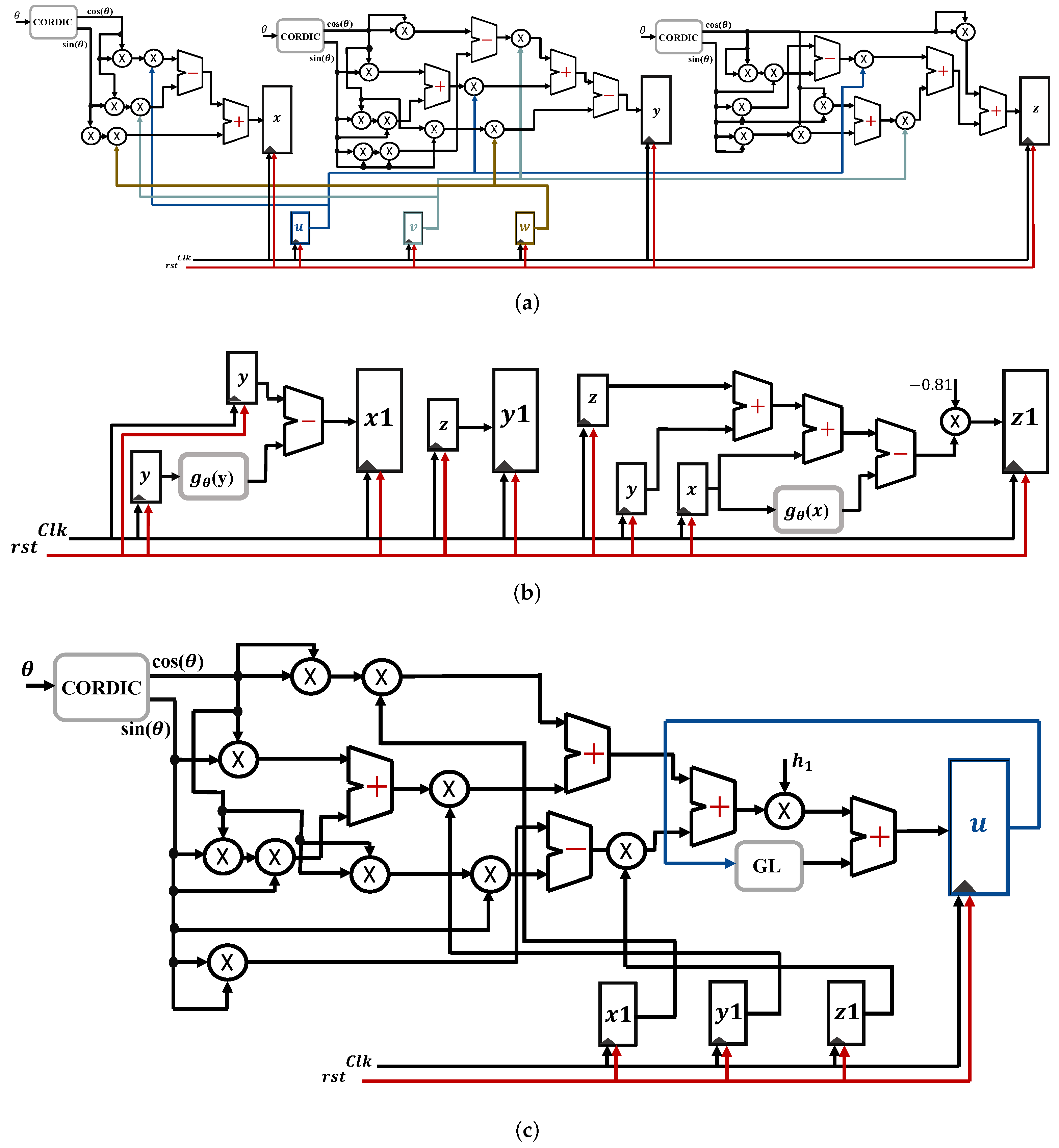
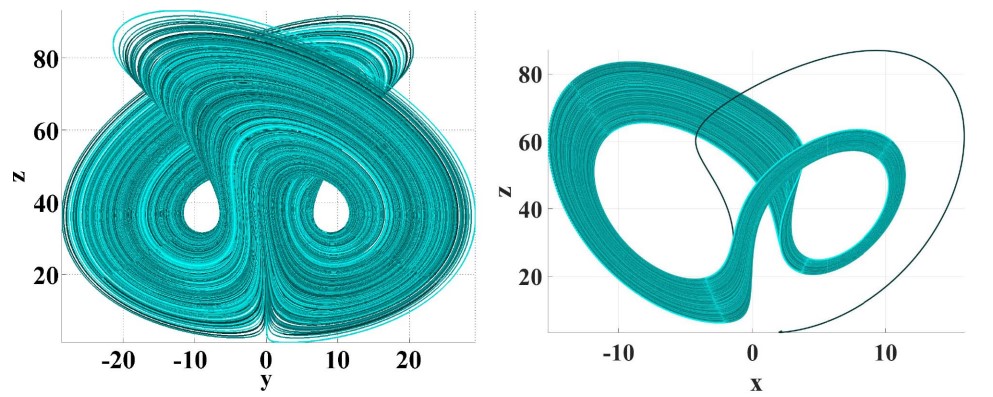
This paper proposes an algorithm and hardware realization of generalized chaotic systems using fractional calculus and rotation algorithms. Enhanced chaotic properties, flexibility, and controllability are achieved using fractional orders, a multi-scroll grid, a dynamic rotation angle(s) in two- and three-dimensional space, and translational parameters. The rotated system is successfully utilized as a Pseudo-Random Number Generator (PRNG) in an image encryption scheme. It preserves the chaotic dynamics and exhibits continuous chaotic behavior for all values of the rotation angle. The

In this paper, an automated universal verification methodology (UVM) tool for rapid functional verification is presented. Now, UVM dominates the verification process but, it is very hard and too complicated to learn. This paper introduces a lightweight UVM tool which allows the user to rapidly verify complex RTL designs and different IPs. Also, it allows the user to perform the simulation for any design under test (DUT). The proposed tool generates the suitable UVM architecture to the DUT with the needed codes. Moreover, it provides the user with statistics about the number of the used classes

This chapter presents results on the most suitable bio-impedance circuits for modeling woody plants. The modified double-shell, the modified triple Cole-Cole, and the traditional wood circuit models are compared for fitting experimentally measured data. Consequently, a modified circuit model is proposed. This model gives the best results for all interelectrode spacing distances when compared to the other circuits. All impedance data have been measured using the research-grade SP150 electrochemical station in the frequency range 0.1 Hz to 200 kHz. The fitting is done using the Zfit of the

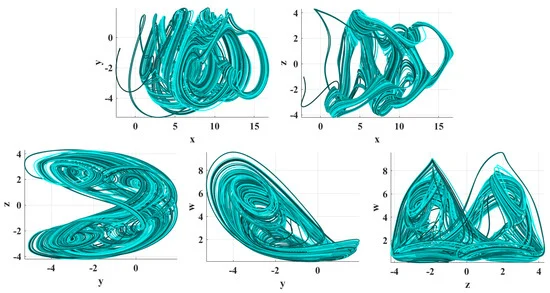
The work in this paper extends a memristive chaotic system with transcendental nonlinearities to the fractional-order domain. The extended system’s chaotic properties were validated through bifurcation analysis and spectral entropy. The presented system was employed in the substitution stage of an image encryption algorithm, including a generalized Arnold map for the permutation. The encryption scheme demonstrated its efficiency through statistical tests, key sensitivity analysis and resistance to brute force and differential attacks. The fractional-order memristive system includes a

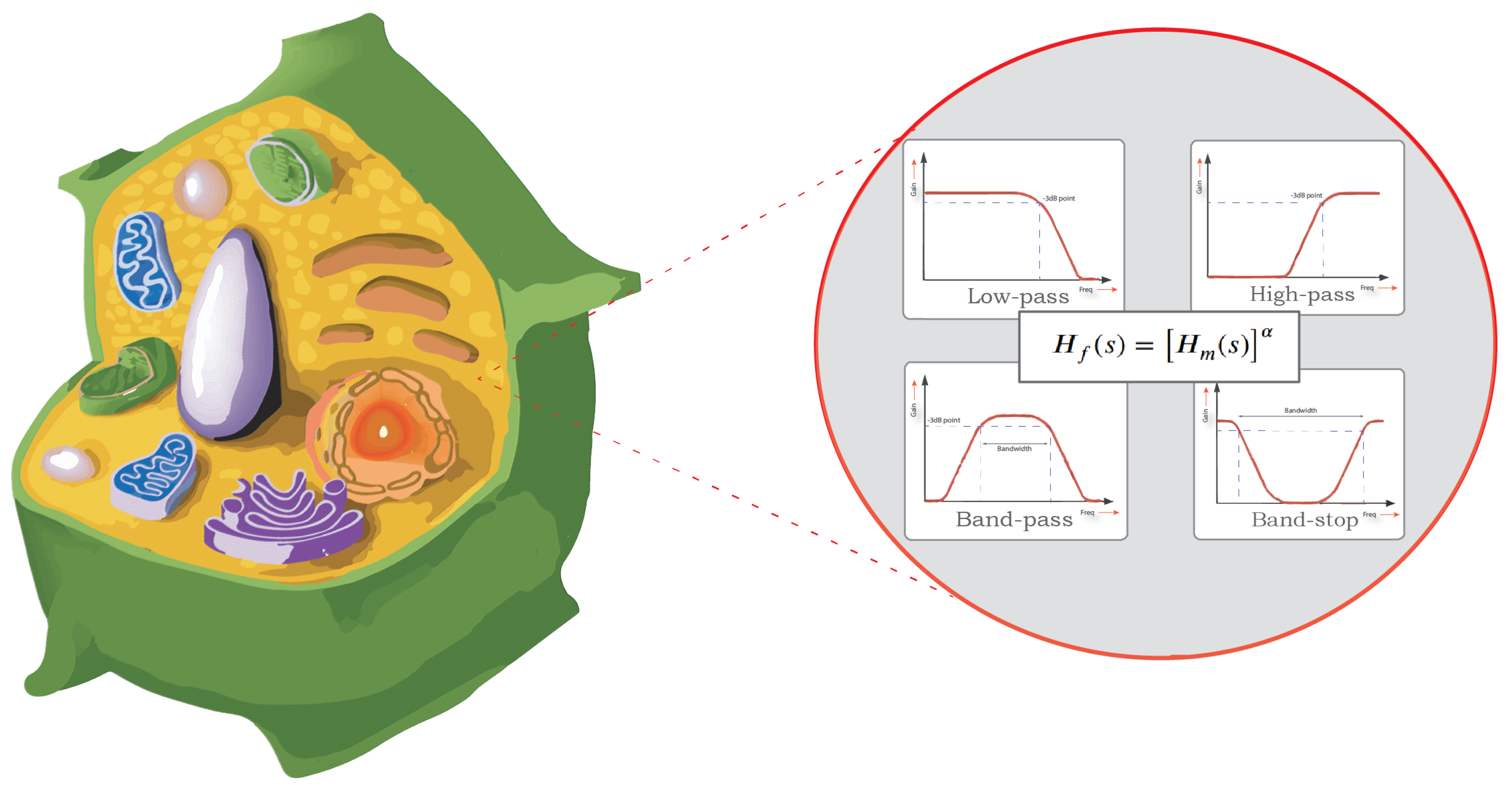
Impedance spectroscopy has became an essential non-invasive tool for quality assessment measurements of the biochemical and biophysical changes in plant tissues. The electrical behaviour of biological tissues can be captured by fitting its bio-impedance data to a suitable circuit model. This paper investigates the use of power-law filters in circuit modelling of bio-impedance. The proposed models are fitted to experimental data obtained from eight different fruit types using a meta-heuristic optimization method (the Water Cycle Algorithm (WCA)). Impedance measurements are obtained using a

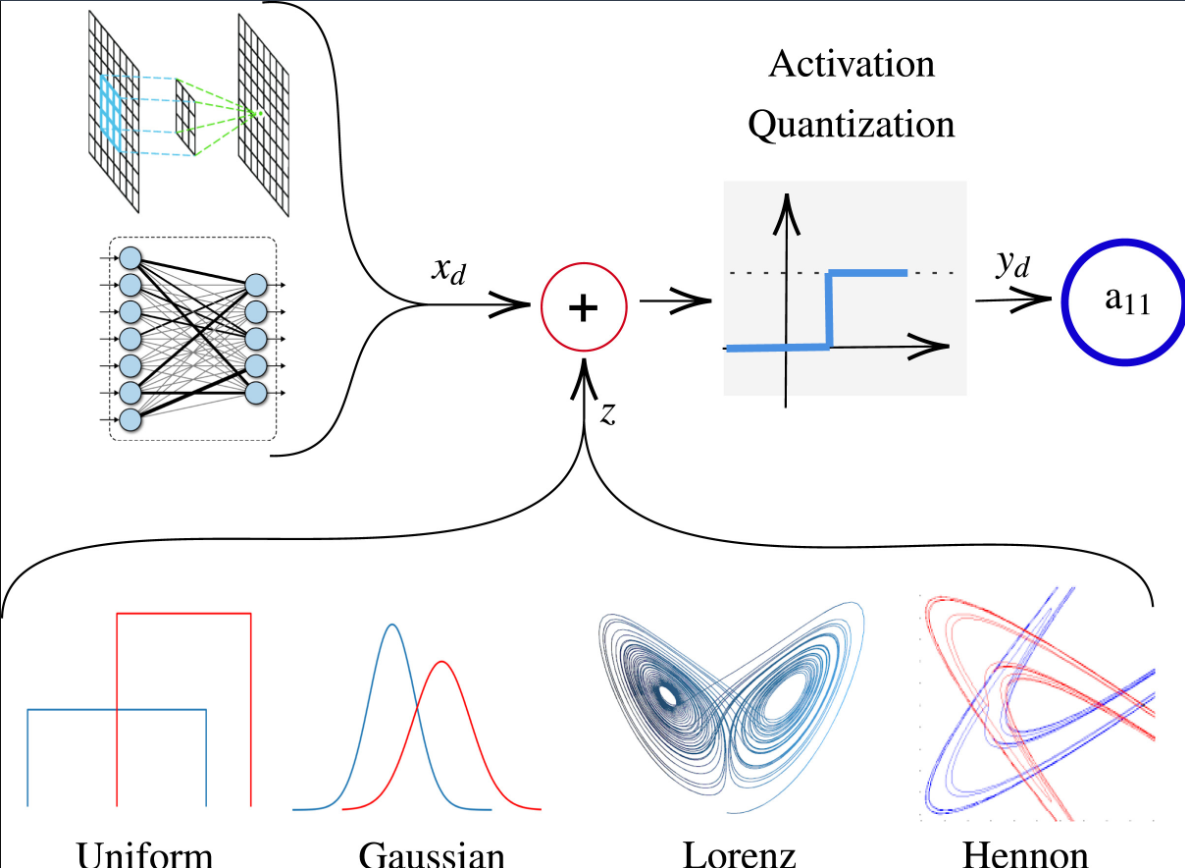
Achieving robustness against adversarial attacks while maintaining high accuracy remains a critical challenge in neural networks. Parameter quantization is one of the main approaches used to compress deep neural networks to have less inference time and less storage memory size. However, quantization causes severe degradation in accuracy and consequently in model robustness. This work investigates the efficacy of stochastic quantization to enhance robustness and accuracy. Noise injection during quantization is explored to understand the impact of noise types and magnitudes on model performance

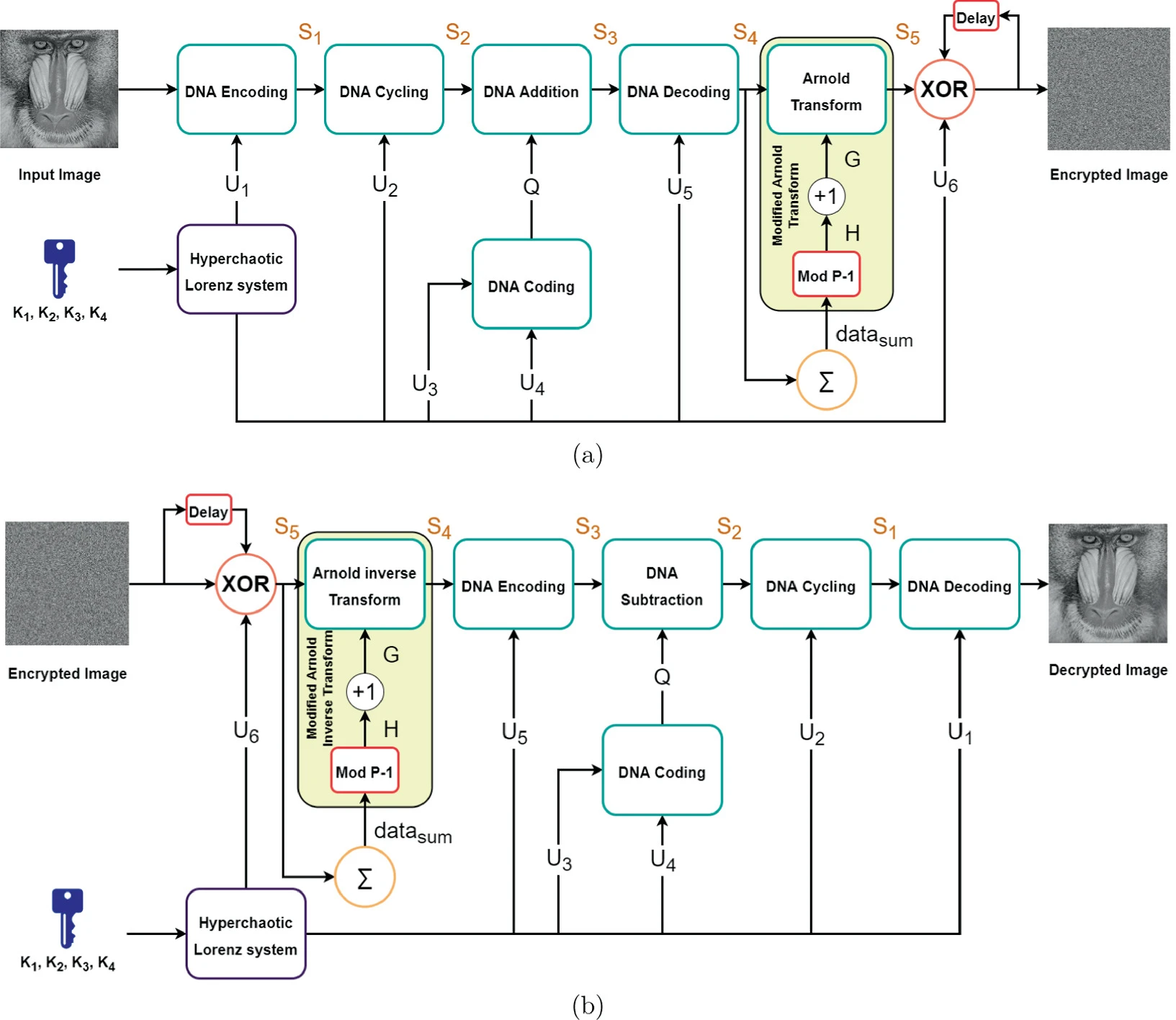
Digital images, which we store and communicate everyday, may contain confidential information that must not be exposed to others. Numerous researches are interested in encryption, which protects the images from ending up in the hands of unauthorized third parties. This paper proposes an image encryption scheme using chaotic systems, DNA manipulation, and a modified Arnold transform. Both DNA manipulation and hyperchaotic Lorenz system are utilized in the substitution of the images’ pixel values. An additional role of hyperchaotic Lorenz system is that it generates the random numbers required

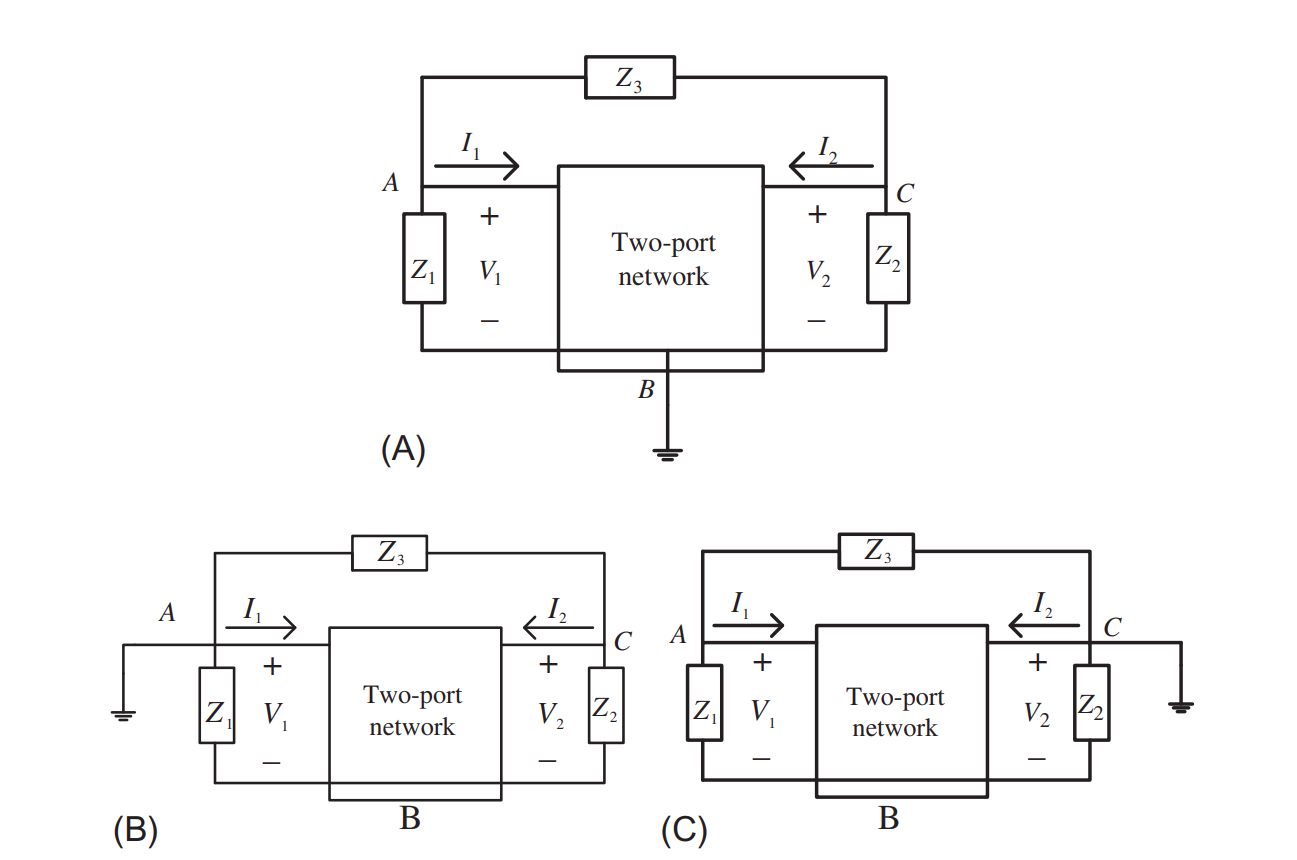
This chapter merges the fractional calculus and two-port networks in oscillator design. The fractional-order elements α and β add extra degrees of freedom that increase the design flexibility and frequency band while providing control over the phase difference. A prototype of the fractional-order two-port network oscillators is introduced. It consists of a general two-port network and three impedances distributed as input, output, and a feedback impedance. Three different two-port network classifications are obtained according to the ground location. This chapter focuses on one of these

Wireless power transfer is becoming an increasingly viable solution for the electrical powering of various electronic gadgets. However, precise outputs are not guaranteed with integer systems, so fractional-order capacitors are vital. This paper studies a four-plate fractional capacitive power transfer system by varying six orders of capacitors between the plates along with the load resistance. A mathematical model based on a 4× 4 mutual fractional capacitance matrix is established for equidistantly placed four identical metal plates. Moreover, the chosen circuit topology is identified and