This paper discusses the implementation sensitivity of chaotic systems added to their widely discussed sensitivities to initial conditions and parameter variation. This sensitivity can cause mismatches in some applications, which require an exact duplication of the system, e.g., chaos-based cryptography, synchronization and communication. Specifically, different implementation cases of three discretized jerk-based chaotic systems and a discrete-time logistic map are presented corresponding to different orders of additions and multiplications. The cases exhibit roughly similar attractor shapes

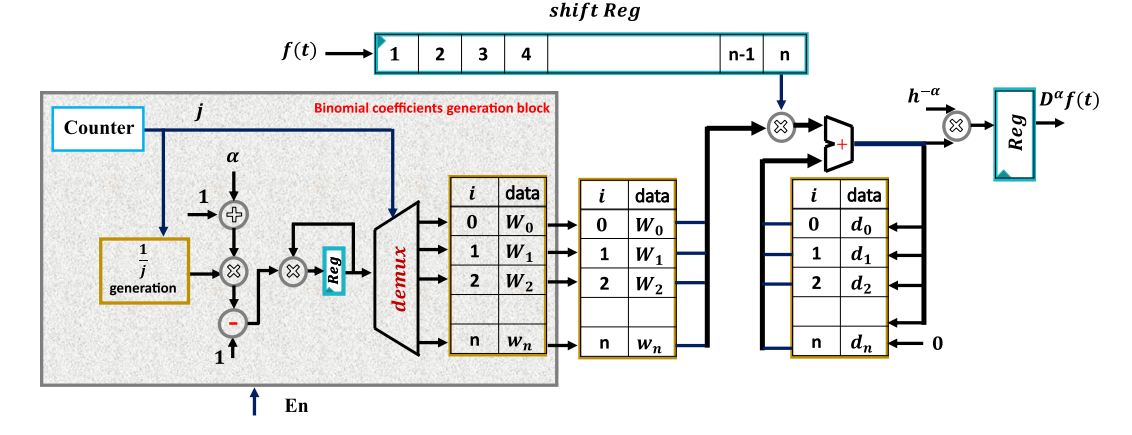
The efficiency of the hardware implementations of fractional-order systems heavily relies on the efficiency of realizing the fractional-order derivative operator. In this work, a generic hardware implementation of the fractional-order derivative based on the Grünwald–Letnikov’s approximation is proposed and verified on a field-programmable gate array. The main advantage of this particular realization is its flexibility in applications which enable easy real-time configuration of the values of the fractional orders, step sizes, and/or other system parameters without changing the hardware

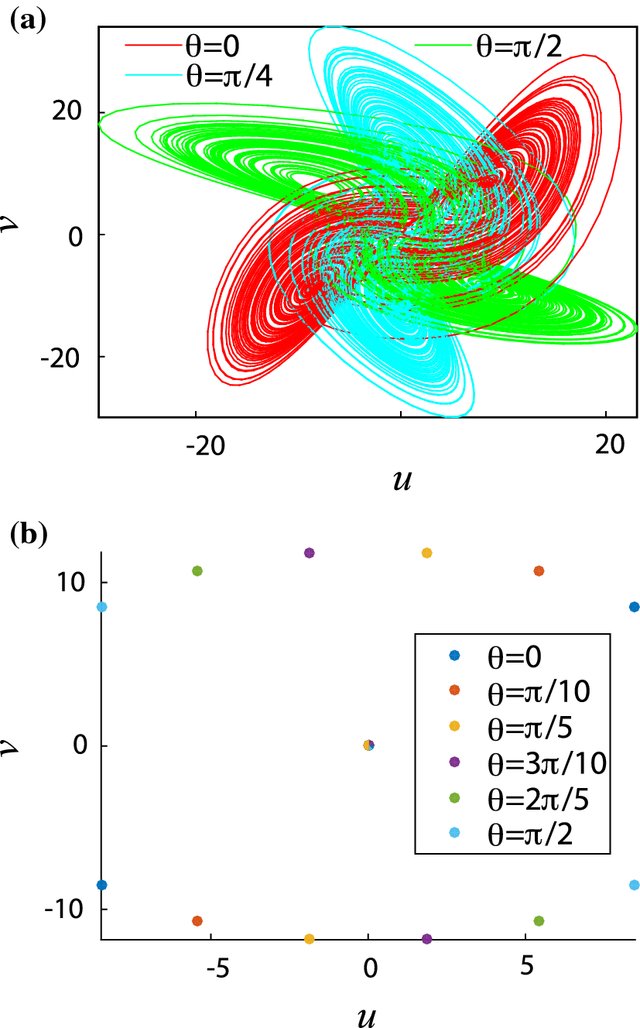
In this work, we demonstrate the possibility of performing two-dimensional rotation on a chaotic system. This enables the rotation of its attractor in space without changing its chaotic dynamics. In particular, the rotated system preserves the same eigenvalues at all equilibrium points and its largest Lyapunov exponent remains unchanged. Two chaotic systems, one of which is the classical Lorenz system, are used to illustrate and validate the rotation operation using numerical simulations and further experimentally using a digital FPGA platform. © 2019, Springer Science+Business Media, LLC

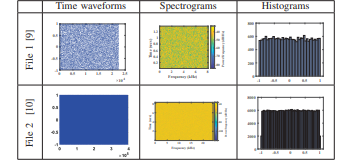
In this paper, we proposed a new technique for designing a dynamic S-box depended on the idea of DNA module and Chaotic system to increase its security. Lorenz chaotic generator is utilized as the chaos part of the proposed design. This design is Tested on the Field Programmable Gate Array (FPGA) for the use of offline speech encryption and decryption in real time. The experimental results are presented on the oscilloscope. The security of the system is also validated through tests on Matlab. © 2019 IEEE.

Chaos is described as a unstable dynamic behavior with dependence on initial conditions. The control and synchronization of chaotic systems requires the knowledge of parameters in advance. Recently researcher's has been shifted from integer order chaotic system to fraction order chaotic system. In this work, based on the stability theory of integer-order linear systems and Lyapunov stability theory, we present some control schemes to achieve a new type of synchronization called inverse generalized synchronization between different dimensional integer and fractional-orders chaotic systems. The

Having an approximate realization of the fractance device is an essential part of fractional-order filter design and implementation. This encouraged researchers to introduce many approximation techniques of fractional-order elements. In this paper, the fractional-order KHN low-pass and high-pass filters are investigated based on four different approximation techniques: Continued Fraction Expansion, Matsuda, Oustaloup, and Valsa. Fractional-order filter fundamentals are reviewed then a comparison is made between the ideal and actual characteristic of the filter realized with each approximation

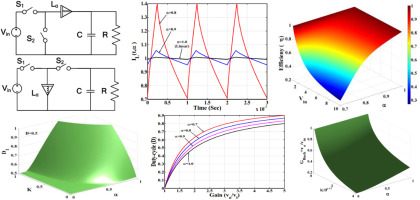
Due to the non-idealities of commercial inductors, the demand for a better model that accurately describe their dynamic response is elevated. So, the fractional order models of Buck, Boost and Buck-Boost DC-DC converters are presented in this paper. The detailed analysis is made for the two most common modes of converter operation: Continuous Conduction Mode (CCM) and Discontinuous Conduction Mode (DCM). Closed form time domain expressions are derived for inductor currents, voltage gain, average current, conduction time and power efficiency where the effect of the fractional order inductor is

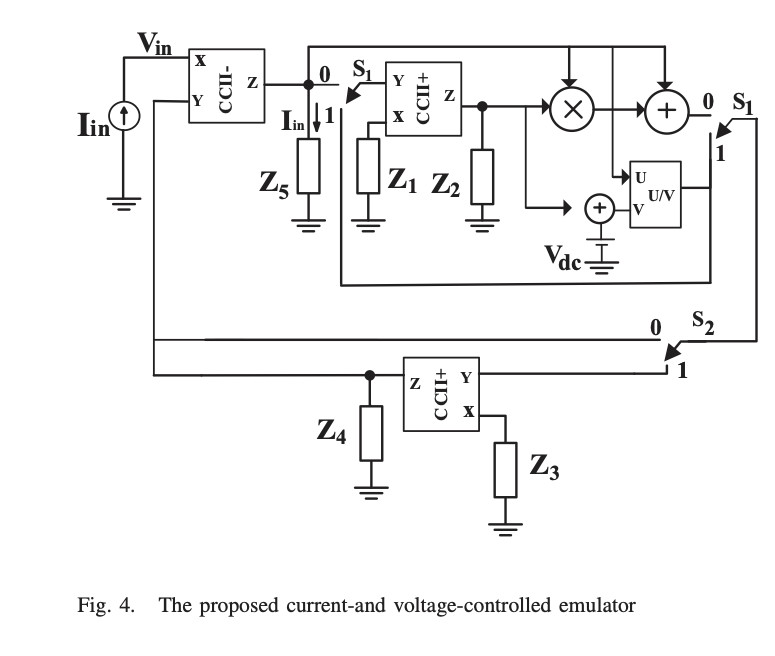
This paper proposes a current-/voltage-controlled universal emulator that can realize any fractional-order memelements (FOME). The proposed emulator consists of second-generation current conveyors (CCII) block, two switches, and a multiplier/divider block. The first switch controls the emulator mode (voltage or current), while, the other controls the type of the emulated FOME. The influence of the fractional-order capacitor (FOC) on the pinched hysteresis loop (PHL) area, is discussed which increases the controllability on the double loop area and the working frequency range. Numerical and

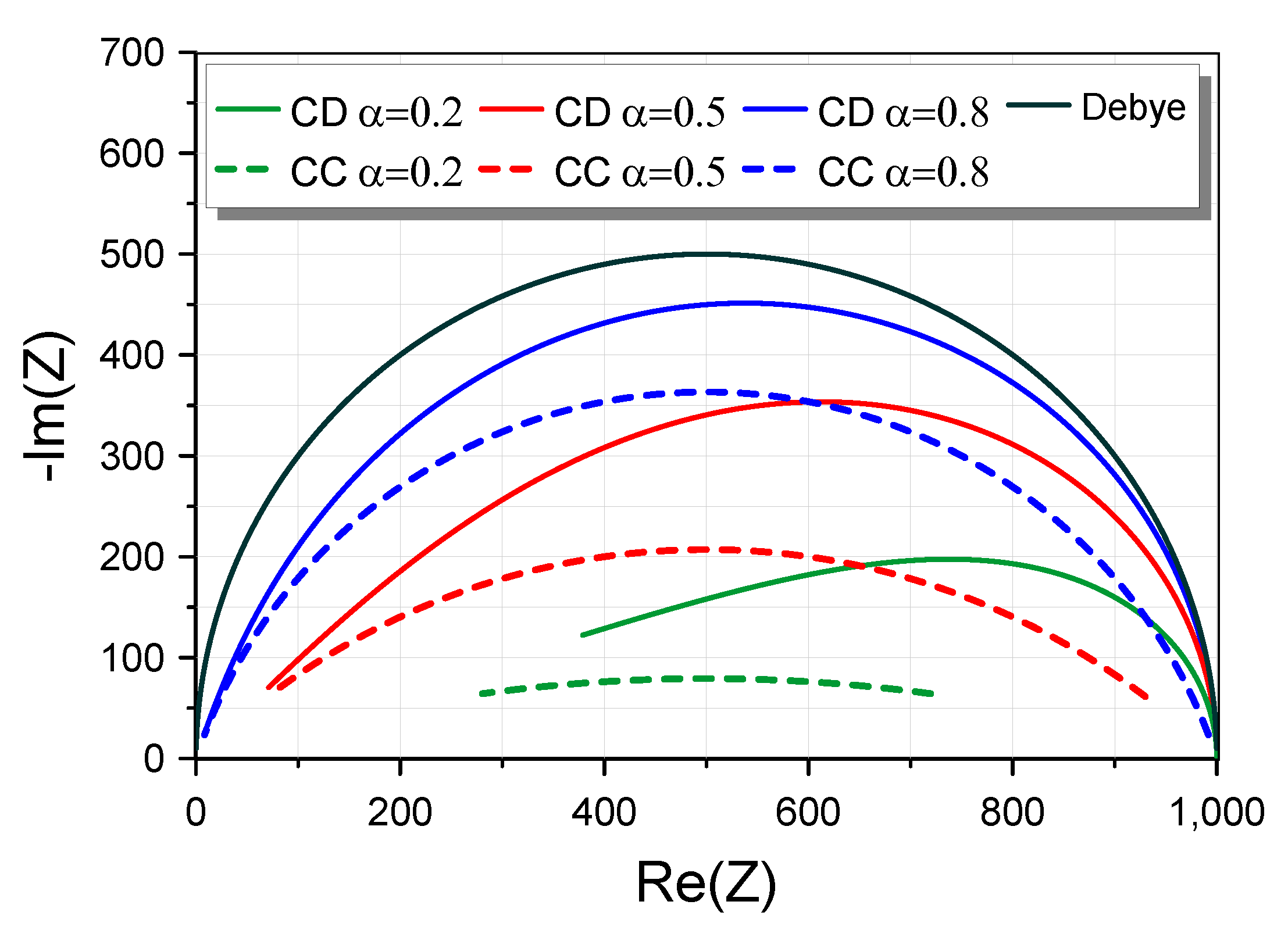
The Cole–Davidson function is an efficient tool for describing the tissue behavior, but the conventional methods of approximation are not applicable due the form of this function. In order to overcome this problem, a novel scheme for approximating the Cole–Davidson function, based on the utilization of a curve fitting procedure offered by the MATLAB software, is introduced in this work. The derived rational transfer function is implemented using the conventional Cauer and Foster RC networks. As an application example, the impedance model of the membrane of mesophyll cells is realized, with

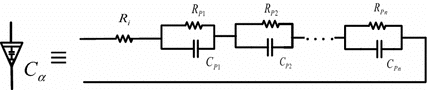
Characterizing and modeling electrical energy storage devices is essential for their proper integration in larger systems. However, basic circuit elements, i.e. resistors, inductors, and capacitors, are not well-suited to explain their complex frequency-dependent behaviors. Instead, fractional-order models, which are based on non-integer-order differential equations in the time-domain and include for instance the constant phase element (CPE), are mathematically more fit to this end. Here, the electrical power and energy of fractional-order capacitance and inductance are derived in both steady