Rates and Effects of Local Minima on Fractional-Order Circuit Model Parameters Extracted from Supercapacitor Discharging Using Least Squares Optimization
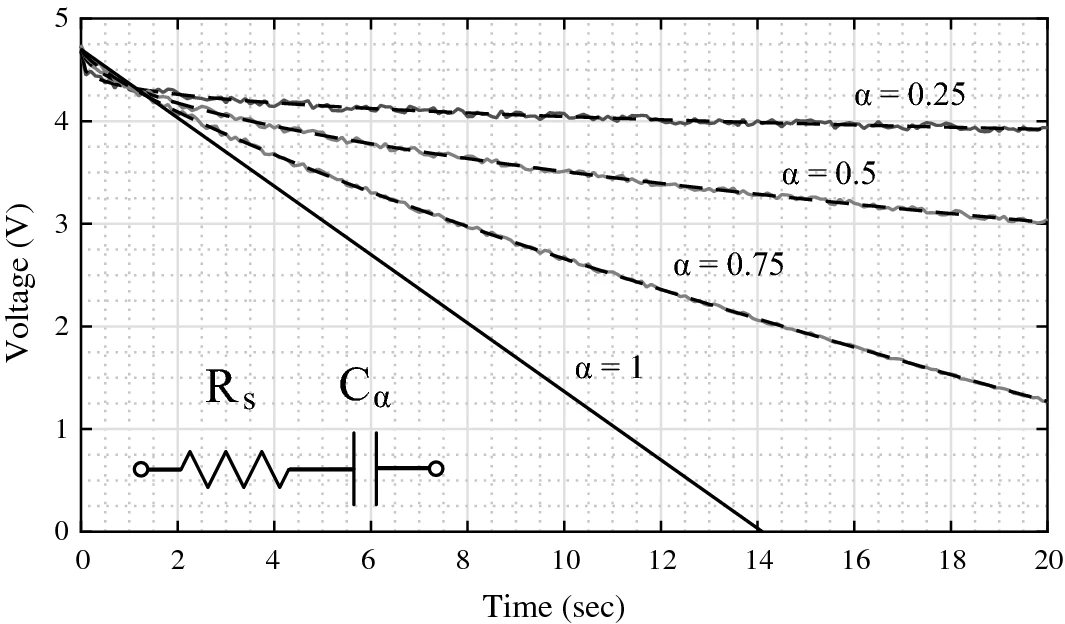
Optimization routines are widely used to numerically determine a set of model parameters that best fit collected experimental data. One recent application of these methods is to extract the fractional-order circuit model parameters that accurately characterize the transient behavior of discharging supercapacitors. However, the variability that these methods introduce to the extracted model parameters must be understood to determine if changes in model parameters are artifacts of the optimization routine or are representative of physical changes in the device under study. In this work, the variability of supercapacitor fractional-order model parameters is quantified when extracted using a nonlinear least squares optimization applied to simulated data (with 0.1–3% noise) and experimental data of their discharging behavior. These results indicate that the local minima problem occurs at a rate of < 1 % for this application, though this problem can be overcome using at least 10 independent executions of the solver to each dataset. The variability of the model parameters using 1000 executions of the solver with 1 and 10 iterates is quantified for both simulated and experimental data, with the 10 iterates showing at least an order of magnitude reduction in the range of returned parameters. © 2018, Springer Science+Business Media, LLC, part of Springer Nature.