
Mechanical Design

Ternary SRAM circuit designs with CNTFETs
Static random-access memory (SRAM) is a cornerstone in modern microprocessors architecture, as it has high power consumption, large area, and high complexity. Also, the stability of the data in the SRAM against the noise and the performance under the radian exposure are main concern issues. To overcome these limitations in the quest for higher information density by memory element, the ternary logic system has been investigated, showing promising potential compared with the conventional binary base. Moreover, carbon nanotube field effect transistor (CNTFET) is a new alternative device with
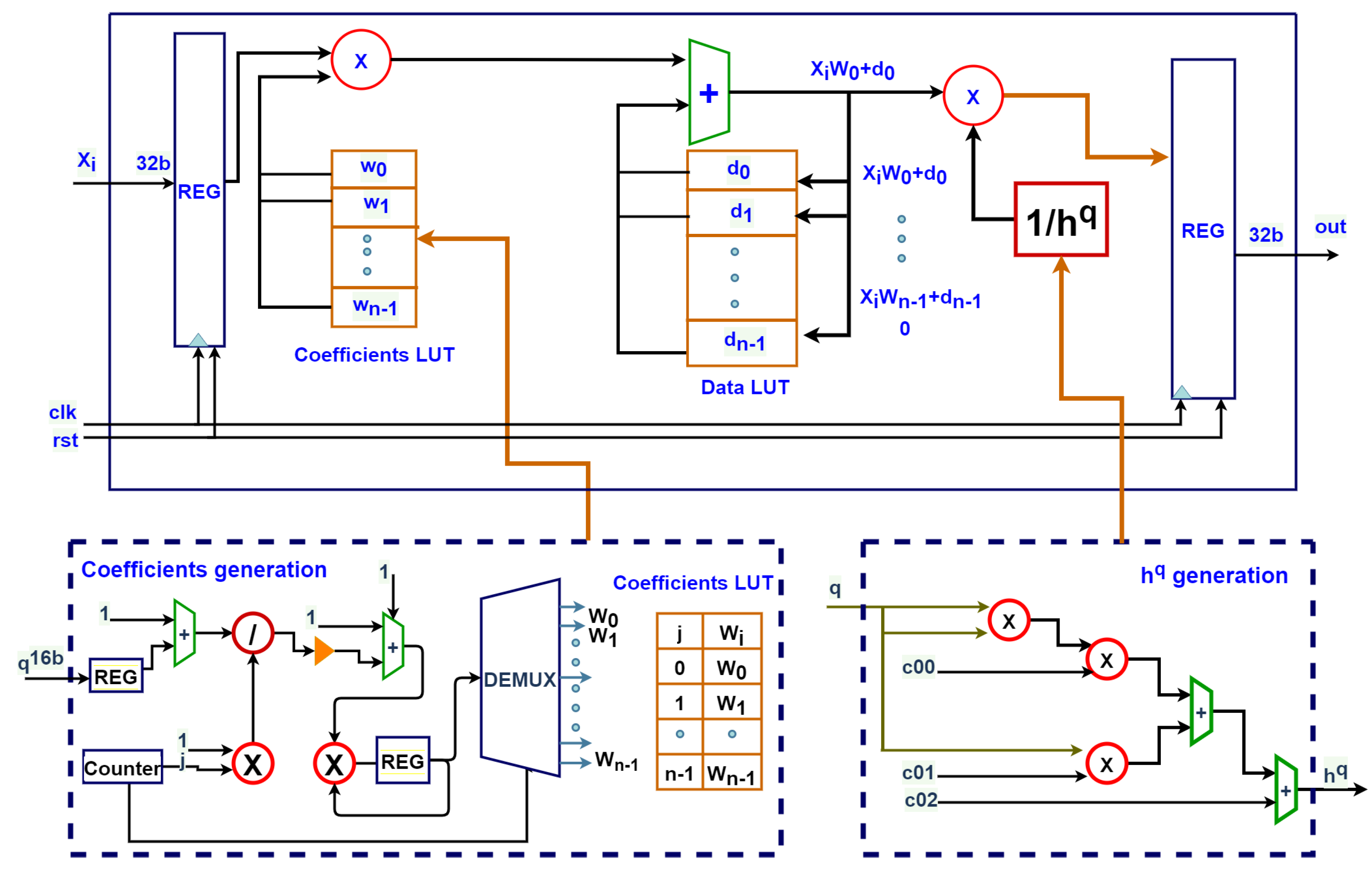
A Unified FPGA Realization for Fractional-Order Integrator and Differentiator
This paper proposes a generic FPGA realization of an IP core for fractional-order integration and differentiation based on the Grünwald–Letnikov approximation. All fractional-order dependent terms are approximated to simpler relations using curve fitting to enable an efficient hardware realization. Compared to previous works, the proposed design introduces enhancements in the fractional-order range covering both integration and differentiation. An error analysis between software and hardware results is presented for sine, triangle and sawtooth signals. The proposed generic design is realized
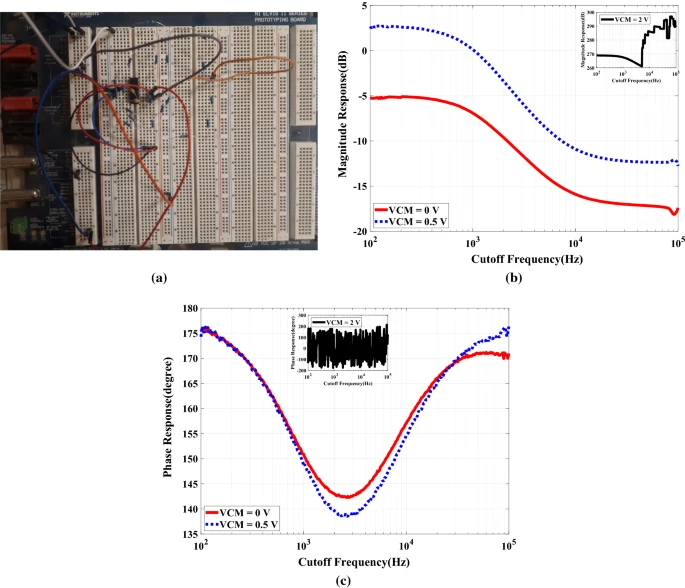
Active and passive sensitivity analysis for the second-order active RC filter families using operational amplifier: a review
This work is a review article that sheds light on the active and passive sensitivities of the active RC filters based on opamp. This work provides a detailed analysis through different filters realization criteria and sensitivity summary tables and quantitative insight by discussing the most significant. However, some are almost forgotten, filters families in the literature over decades. A detailed mathematical analysis for the passive sensitivity to compare the filters’ realizations is presented. The concept of dealing between filter design theory and filter design circuit realization is
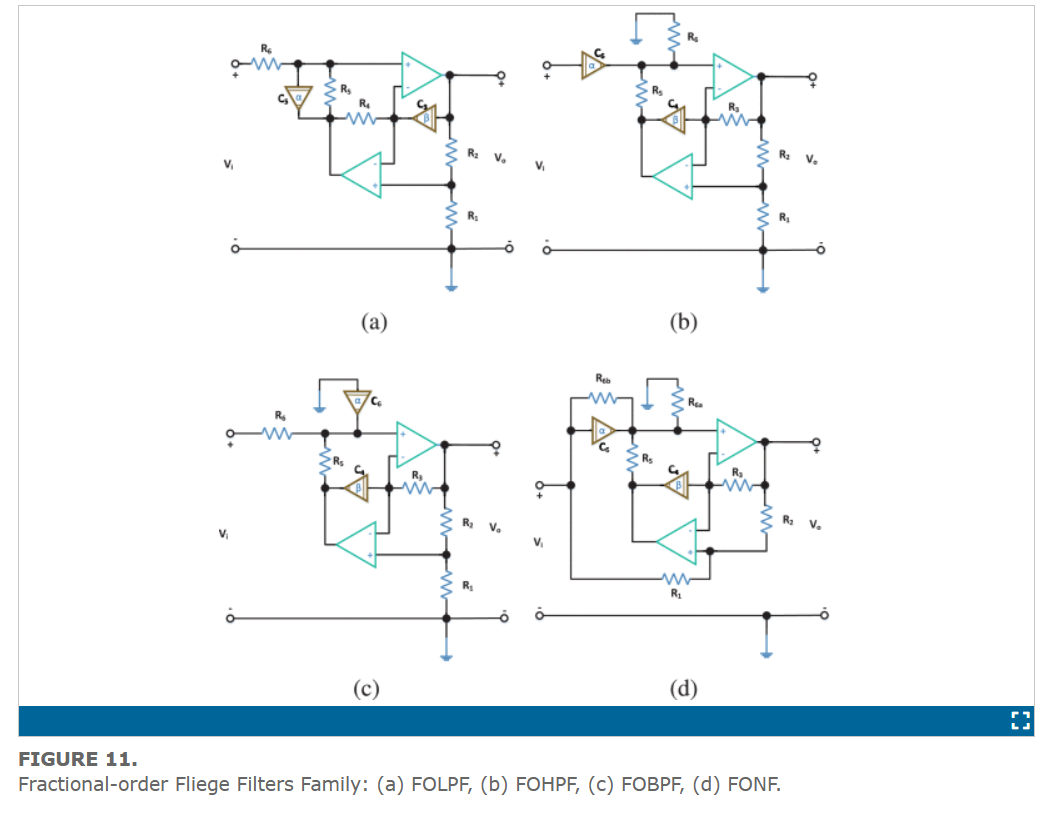
On the Design Flow of the Fractional-Order Analog Filters Between FPAA Implementation and Circuit Realization
This work explicitly states the design flows of the fractional-order analog filters used by researchers throughout the literature. Two main flows are studied: the FPAA implementation and the circuit realization. Partial-fraction expansion representation is used to prepare the approximated fractional-order response for implementation on FPAA. The generalization of the second-order active RC analog filters based on opamp from the integer-order domain to the fractional-order domain is presented. The generalization is studied from both mathematical and circuit realization points of view. It is
FPGA REALIZATION OF COMPLEX LOGISTIC MAP FRACTAL BEHAVIOR
This paper studies the capability of digital architecture to mimic fractal behavior. As chaotic attractors realized digitally had opened many tracks, digital designs mimicking fractals may ultimately achieve the same. This study is based on a complex single-dimensional discrete chaotic system known as the generalized positive logistic map. The fractals realized from this system are linked to the results of the mathematical analysis to understand the fractal behavior with different variations. A digital hardware architecture manifesting the fractal behavior is achieved on FPGA, showing a
CNTFET-Based Ternary Multiply-and-Accumulate Unit
Multiply-Accumulate (MAC) is one of the most commonly used operations in modern computing systems due to its use in matrix multiplication, signal processing, and in new applications such as machine learning and deep neural networks. Ternary number system offers higher information processing within the same number of digits when compared to binary systems. In this paper, a MAC is proposed using a CNTFET-based ternary logic number. Specifically, we build a 5-trit multiplier and 10-trit adder as building blocks of two ternary MAC unit designs. The first is a basic MAC which has two methods to
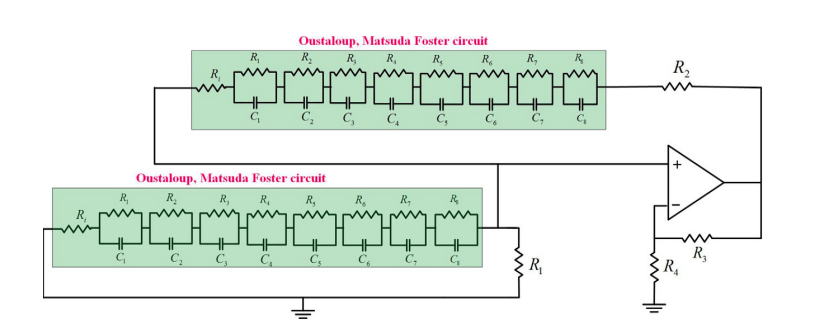
On the Approximation of Fractional-Order Circuit Design
Despite the complex nature of fractional calculus, it is still fairly possible to reduce this complexity by using integer-order approximation. Each integer-order approximation has its own trade-offs from the complexity, sensitivity, and accuracy points of view. In this chapter, two different fractional-order electronic circuits are studied: the Wien oscillator and the CCII-based KHN filter with two different fractional elements of orders α and β. The investigation is concerned with changes in the response of these two circuits under two approximations: Oustaloup and Matsuda. A detailed review
An Automated Lightweight UVM Tool
In this paper, an automated universal verification methodology (UVM) tool for rapid functional verification is presented. Now, UVM dominates the verification process but, it is very hard and too complicated to learn. This paper introduces a lightweight UVM tool which allows the user to rapidly verify complex RTL designs and different IPs. Also, it allows the user to perform the simulation for any design under test (DUT). The proposed tool generates the suitable UVM architecture to the DUT with the needed codes. Moreover, it provides the user with statistics about the number of the used classes
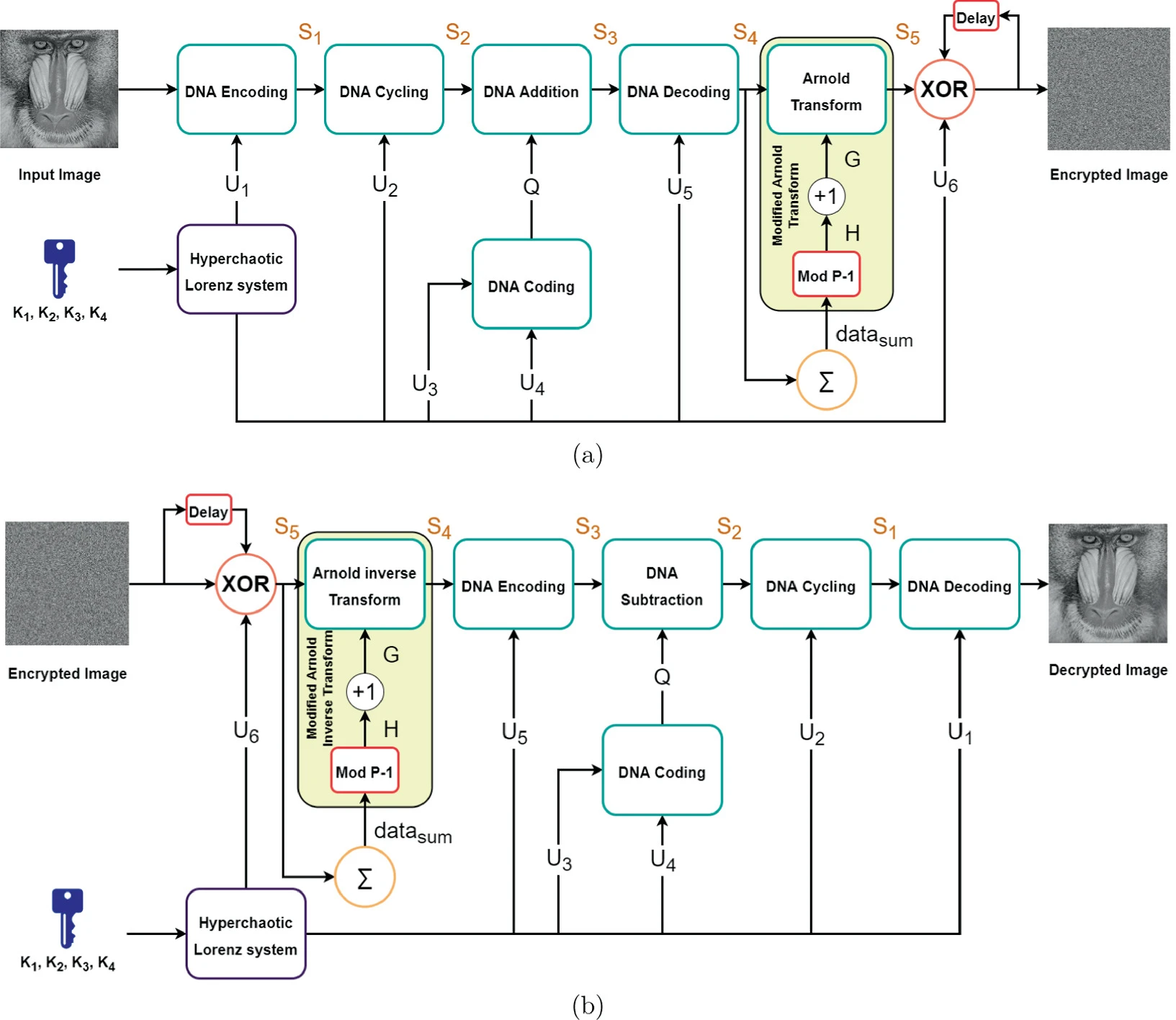
Chaos-Based Image Encryption Using DNA Manipulation and a Modified Arnold Transform
Digital images, which we store and communicate everyday, may contain confidential information that must not be exposed to others. Numerous researches are interested in encryption, which protects the images from ending up in the hands of unauthorized third parties. This paper proposes an image encryption scheme using chaotic systems, DNA manipulation, and a modified Arnold transform. Both DNA manipulation and hyperchaotic Lorenz system are utilized in the substitution of the images’ pixel values. An additional role of hyperchaotic Lorenz system is that it generates the random numbers required
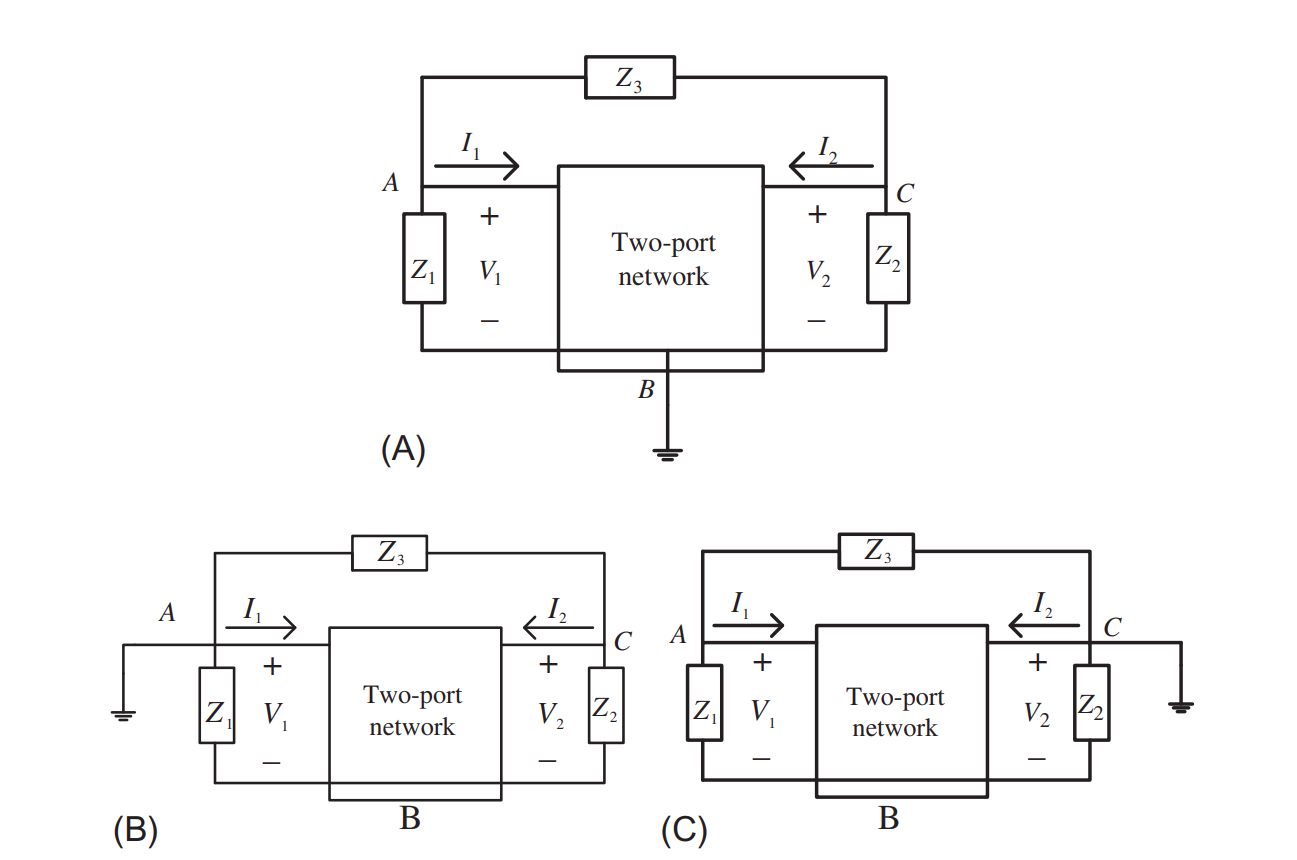
Survey on Two-Port Network-Based Fractional-Order Oscillators
This chapter merges the fractional calculus and two-port networks in oscillator design. The fractional-order elements α and β add extra degrees of freedom that increase the design flexibility and frequency band while providing control over the phase difference. A prototype of the fractional-order two-port network oscillators is introduced. It consists of a general two-port network and three impedances distributed as input, output, and a feedback impedance. Three different two-port network classifications are obtained according to the ground location. This chapter focuses on one of these