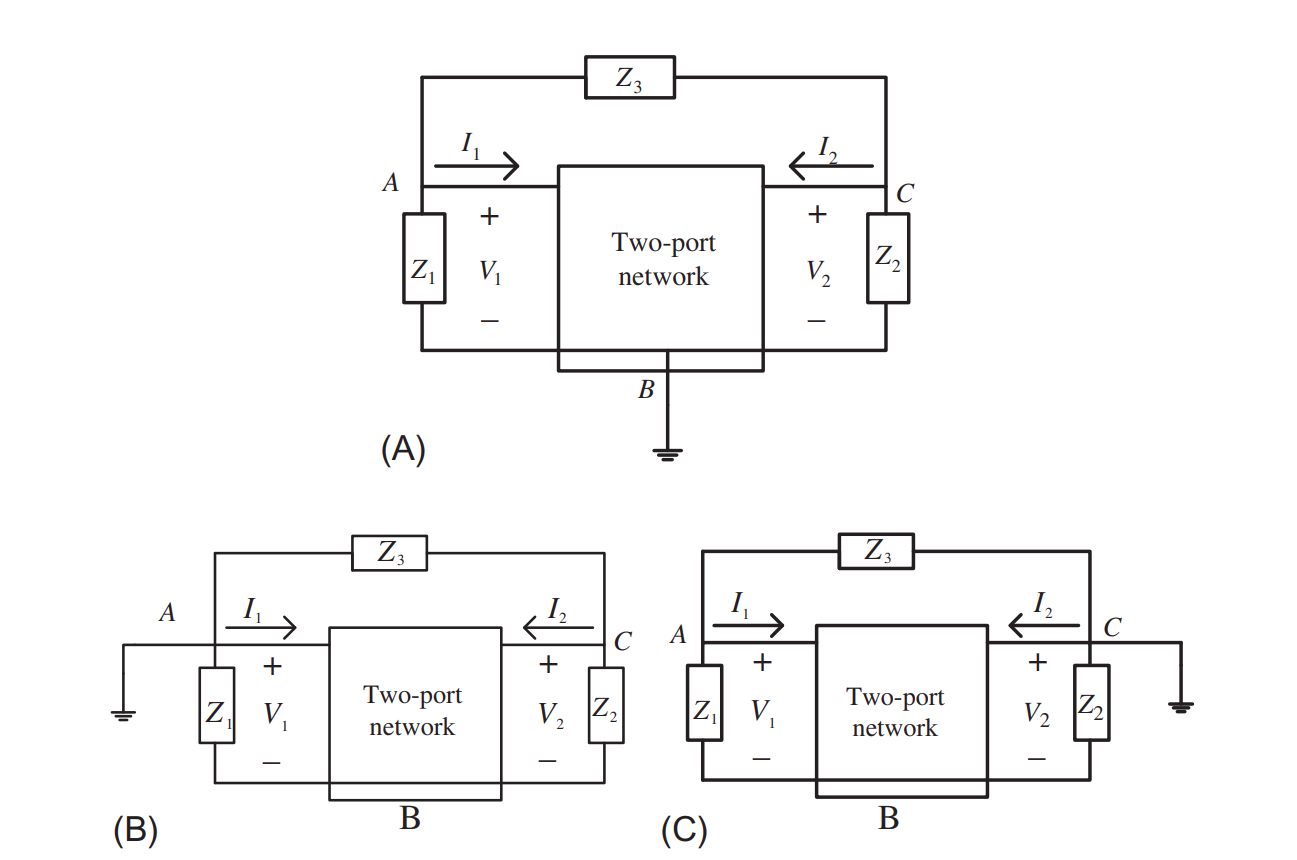
This chapter merges the fractional calculus and two-port networks in oscillator design. The fractional-order elements α and β add extra degrees of freedom that increase the design flexibility and frequency band while providing control over the phase difference. A prototype of the fractional-order two-port network oscillators is introduced. It consists of a general two-port network and three impedances distributed as input, output, and a feedback impedance. Three different two-port network classifications are obtained according to the ground location. This chapter focuses on one of these

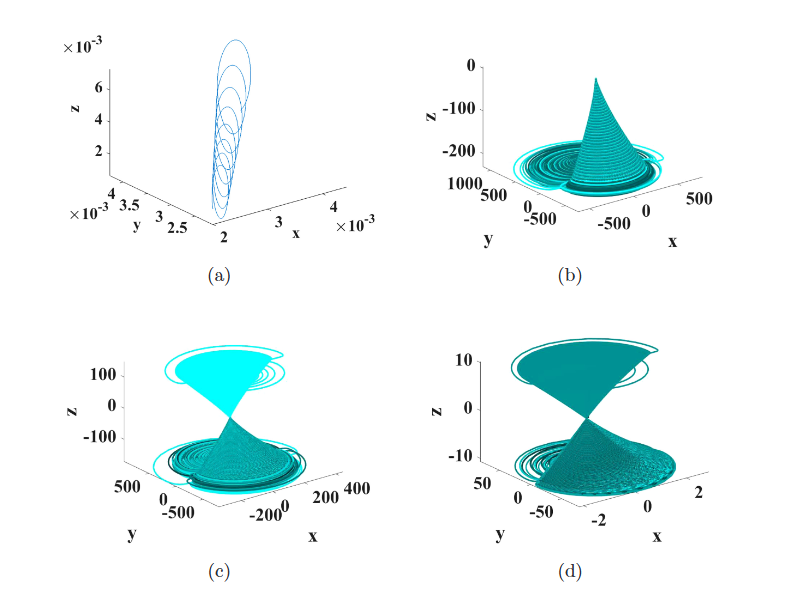
We introduce a new chaotic system with nonhyperbolic equilibrium and study its sensitivity to different numerical integration techniques prior to implementing it on an FPGA. We show that the discretization method used in numerically integrating the set of differential equations in MATLAB and Mathematica does not yield chaotic behavior except when a low accuracy Euler method is used. More accurate higher-order numerical algorithms (such as midpoint and fourth-order Runge-Kutta) result in divergence in both MATLAB and Mathematica (but not Python), which agrees with the divergence observed in an

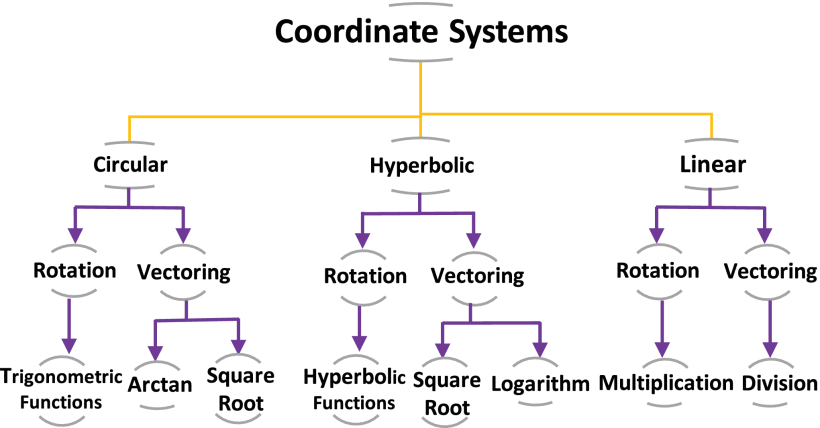
Coordinate Rotation Digital Computer (CORDIC) is a robust iterative algorithm that computes many transcendental mathematical functions. This paper proposes a reconfigurable CORDIC hardware design and FPGA realization that includes all possible configurations of the CORDIC algorithm. The proposed architecture is introduced in two approaches: multiplier-less and single multiplier approaches, each with its advantages. Compared to recent related works, the proposed implementation overpasses them in the included number of configurations. Additionally, it demonstrates efficient hardware utilization

Over the years, The detection and tracking of Vulnerable Road Users (VRUs) have become one of the most critical features of self-driving car components. Because of its processing efficiency and better detection algorithms, tracking-by-detection appears to be the best paradigm. In this paper, a detection-based tracking approach is presented for Multiple VRU Tracking of video from an inside-vehicle camera in real-time. YOLOv4 scans every frame to detect VRUs first, then Simple Online and Realtime Tracking with a Deep Association Metric (Deep SORT) algorithm, which is customized for multiple VRU

Biometric security has been developed in recent years with the emergence of cancellable biometric concepts. The idea of the cancellable biometric traits is concerned with creating encrypted or distorted traits of the original ones to protect them from hacking techniques. So, encrypted or distorted biometric traits are stored in databases instead of the original ones. This can be accomplished through non-invertible transforms or encryption schemes. In this paper, a cancellable face recognition algorithm is introduced based on face image encryption through a fractional-order multi-scroll chaotic

The DC motor is one of the simplest electrical machines used in industry since it is controlled by direct voltages and currents. These configurations have various advantages, allowing the machine to be adapted to the constraints of its specific application. The present chapter analyzes the DC motor with separate excitation without the use of a speed sensor to approximate the rotor speed. An analysis of the stability of the rotor speed estimation is performed. Enhanced control of the direct action is integrated into the adaptive observer to decrease the roundness capability of the model and

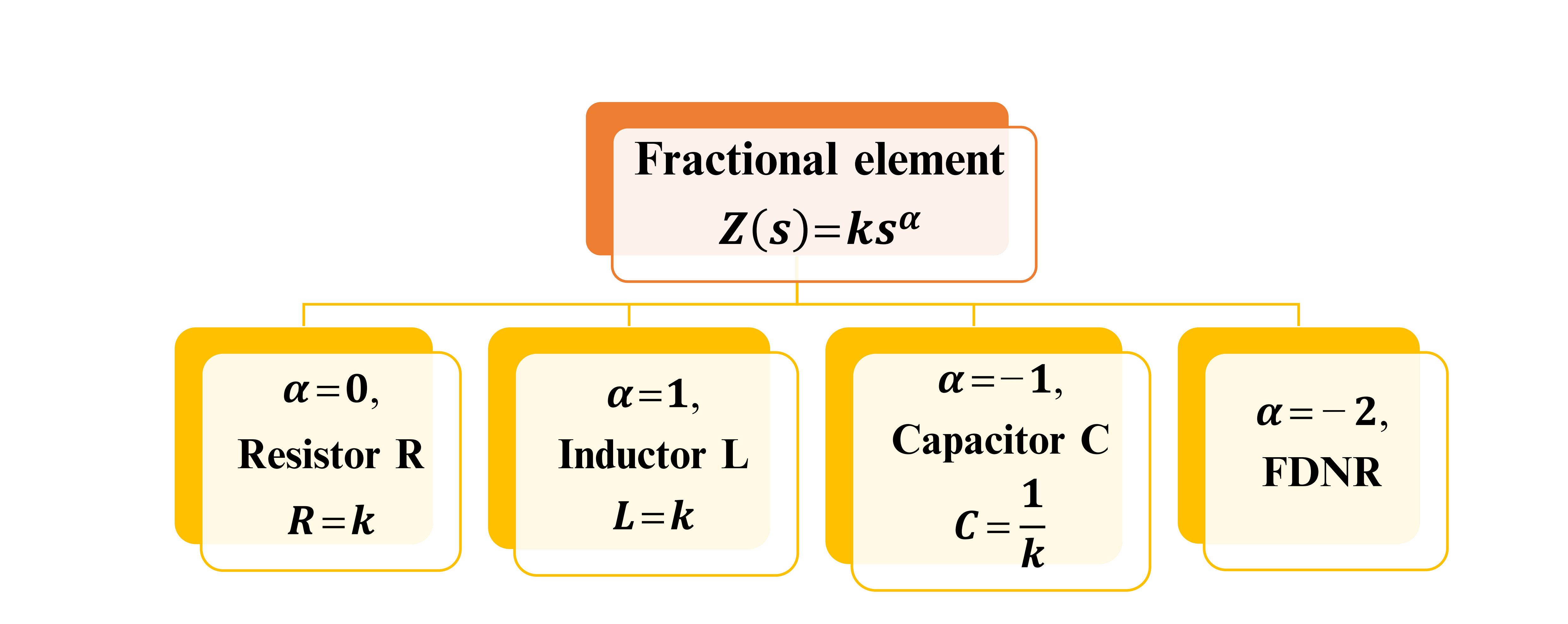
One of the advantages of fractional order is the extra degree of freedom added by the fractional-order parameters, which enrich the analysis with more details in new dimensions. This chapter introduces factional-order conventional filters of orders α, 2α, and 3α. The general transfer functions of continuous-time filters (low-pass, high-pass, and band-pass filters) to the noninteger-order (fractional-order) domain are investigated. Also, mathematical expressions for the maximum and minimum frequencies, the half power frequencies, and the right-phase frequencies are derived. In addition, the

Chua postulated a new element called a memristor, contributing flux and charge link. The main characteristic of the memristor is a pinched hysteresis double loop with one pinched point. The memristor’s realization in the fractional-order domain increases the hysteresis loop area’s controllability and frequency range. Besides, the fractional-higher-order memristor is realized, achieving more than a pinched point with changes of the pinched point’s location at different values of a. The commercial memristor device is absent until now. For this purpose, scientists concentrated on modeling the

Chaos theory describes the dynamical systems which exhibit unpredictable, yet deterministic, behavior. Chaotic systems have a remarkable importance in both modeling and information processing in many fields. Fractional calculus has also become a powerful tool in describing the dynamics of complex systems such as fractional order (FO) chaotic systems. The FO parameter adds extra degrees of freedom which increases the design flexibility and adds more control on the design. The extra parameters increase the chaotic range. This chapter provides a review of several generalized discrete time one

Fractional-order Modelling of Dynamic Systems with Applications in Optimization, Signal Processing and Control introduces applications from a design perspective, helping readers plan and design their own applications. The book includes the different techniques employed to design fractional-order systems/devices comprehensively and straightforwardly. Furthermore, mathematics is available in the literature on how to solve fractional-order calculus for system applications. This book introduces the mathematics that has been employed explicitly for fractional-order systems. It will prove an