
Innovation, Entrepreneurship and Competitiveness
Ethiopian Dam Optimum Hydraulic Operating Conditions to Reduce Unfavorable Impacts on Downstream Countries
As noted by several researchers, the Grand Ethiopian Renaissance Dam (GERD) on the Blue Nile River is expected to have unfavorable consequences for downstream countries like Egypt and Sudan. To limit GERD's negative effects on downstream countries, its operation should be secure, and its upstream water level should be ideal. However, none of the studies carried out the ideal operating scenarios from the perspective of controlling the number of gate openings. Accordingly, this study evaluates the optimal operating scenarios of the GERD and its impact on downstream countries by adopting a
Prediction model for the compressive strength of green concrete using cement kiln dust and fly ash
Integrating artificial intelligence and green concrete in the construction industry is a challenge that can help to move towards sustainable construction. Therefore, this research aims to predict the compressive strength of green concrete that includes a ratio of cement kiln dust (CKD) and fly ash (FA), then recommend the optimum sustainable mixture design. The artificial neural network (ANN) and multiple linear regression techniques are used to build prediction models and statistics using MATLAB and IBM SPSS software. The input parameters are based on 156 data points of concrete components

Decision Support Framework for the Choice of Delay Analysis Techniques Used in Extension of Time Claims
One of the inevitable challenges that face the construction industry is the delay of project completion. The current state of the industry makes the need for delay analysis apparent, however the process of choosing the most reliable delay analysis technique can get very complex in some situations. This research aims to develop a framework to identify and analyze the most important factors to consider when choosing a delay analysis technique. The most reliable technique is decided based on a weighted multicriteria decision matrix. The proposed numerical weight for each factor and the pointing
Optimizing the coagulation/flocculation process for the treatment of slaughterhouse and meat processing wastewater: experimental studies and pilot-scale proposal
The slaughterhouse industry generates substantial wastewater rich in proteins, lipids, fibers, and carbohydrates. This study integrates experimental investigations into artificial neural network (ANN) optimization and commerce design studies for treating slaughterhouse and meat processing wastewater (SMW). Batch coagulation/flocculation experiments identified optimal conditions for three coagulants: Ferric Chloride (FeCl3·6H2O), Poly Aluminum Chloride (PAC), and Aluminum Sulfate Al2(SO4)3, aiming for optimum removal of chemical oxygen demand (COD), total suspended solids (TSS), and total
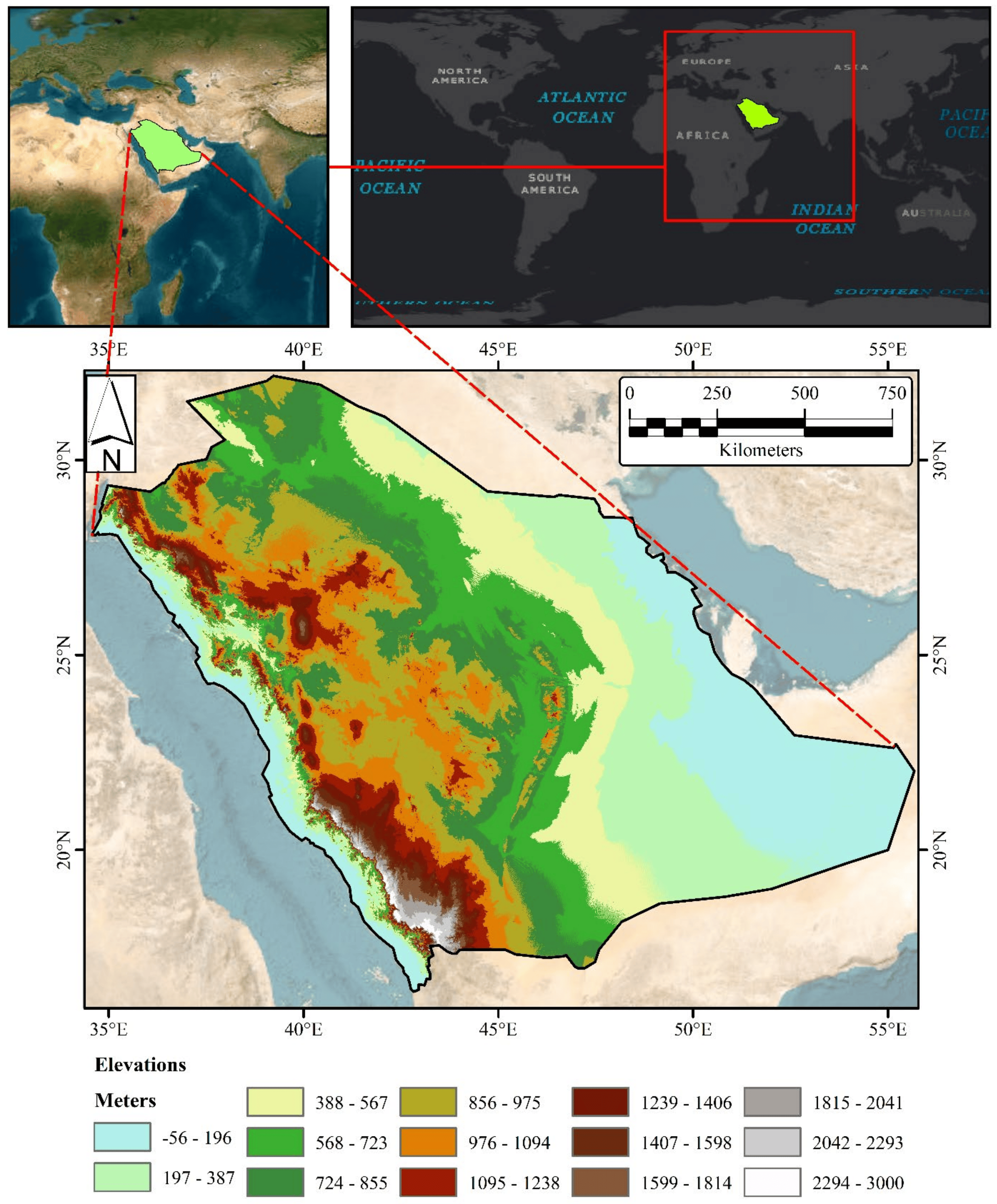
Evaluation of Geospatial Interpolation Techniques for Enhancing Spatiotemporal Rainfall Distribution and Filling Data Gaps in Asir Region, Saudi Arabia
Providing an accurate spatiotemporal distribution of rainfall and filling data gaps are pivotal for effective water resource management. This study focuses on the Asir region in the southwest of Saudi Arabia. Given the limited accuracy of satellite data in this arid/mountain-dominated study area, geospatial interpolation has emerged as a viable alternative approach for filling terrestrial records data gaps. Furthermore, the irregularity in rain gauge data and the yearly spatial variation in data gaps hinder the creation of a coherent distribution pattern. To address this, the Centered Root
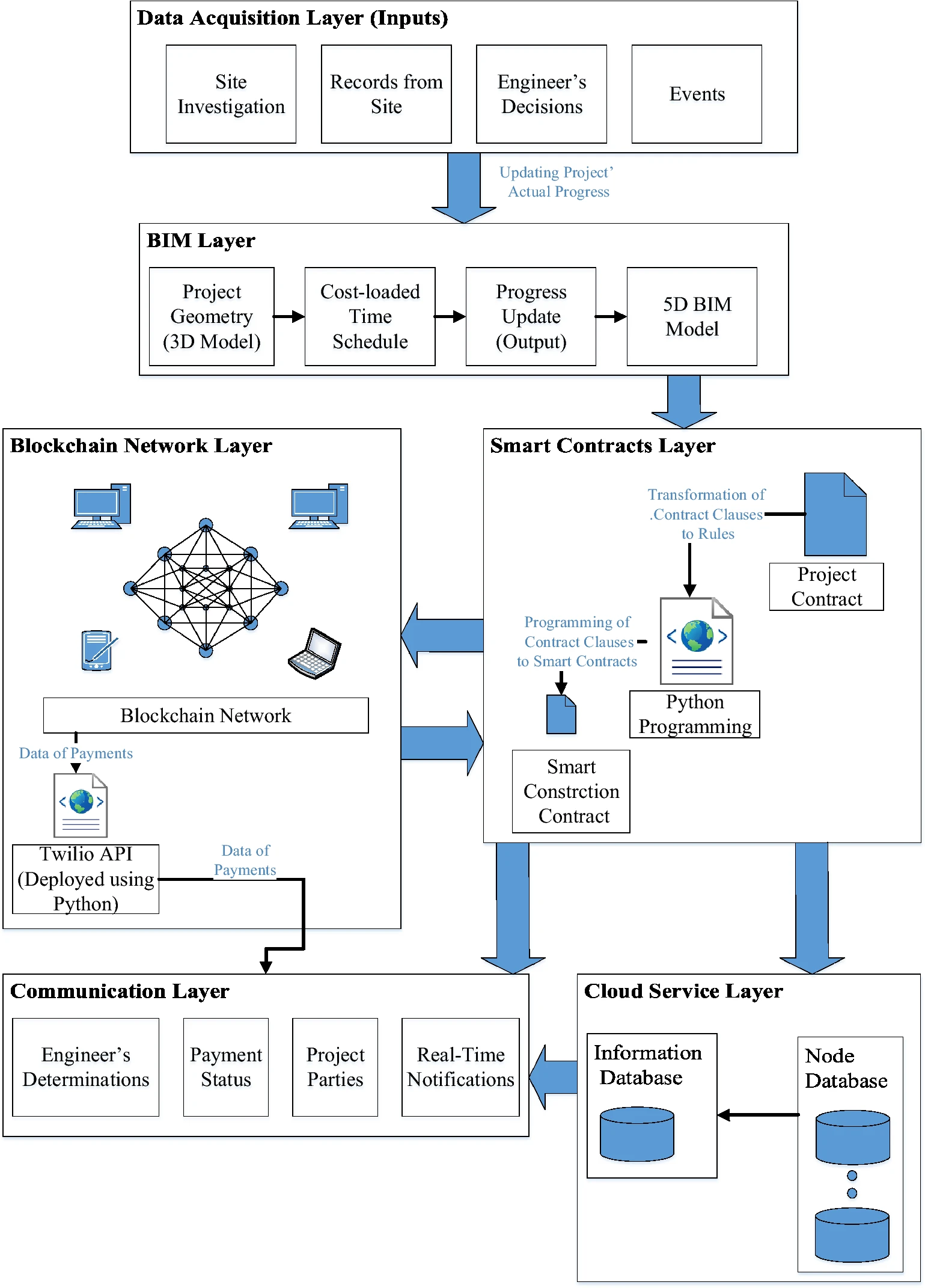
A framework for smart construction contracts using BIM and blockchain
Poor payment practices are perceived as one of the biggest challenges facing the construction industry. Since payments are issued according to project contract terms, the project’s cash flow is inherently affected by the contract and how parties fulfill their obligations. This research proposes a framework for payment automation in construction projects to achieve smart construction contracts. Payments are automatically issued upon satisfying contract conditions using blockchain. Cryptocurrency is proposed to be utilized in the framework to execute the contract terms with no need for a third
Impact assessment of implementing virtual reality in the Egyptian construction industry
Construction projects in Egypt are becoming more complex as the need for mega projects increases to meet the Egyptian 2030 vision. Meanwhile, the advancement of Virtual Reality technologies is apparent in the 21st century. This paper aims to assess the impact of implementing virtual reality in the Egyptian construction industry. An application using Fuzor VDC and Oculus Quest 2 has been developed elaborating the technology's use. The application includes 4D simulation and meetings in virtual reality. Furthermore, a survey is conducted to measure the impact of implementation on key project
The Psychological Impact of University Brand Equity Using Firm Generated EWOM on Students’ Satisfaction: The Moderating Effect of Gender
This study uses firm-generated "electronic word of mouth (eWOM)" and students' satisfaction to analyse the effect of university brand equity. Four aspects of brand equity—"awareness, positioning, perceived quality, and trustworthiness"—are examined by the conceptual framework. It also examines how gender influences the relationship between student satisfaction and institution brand equity. At Nile University in Cairo, Egypt, the study used an exploratory survey methodology with a sample of 295 students from its four schools of "business administration, computer science, engineering, and
Organizational learning via gamification for employer brand management
Purpose: This paper aims to deepen our understanding of how serious games could be used for learning in organizations to empower brand performance and image sustaining competitive advantage from a Resource Based View (RBV) perspective and to examine the practical implications of the evolving technologies for employers. Design/methodology/approach: The research methodology is based on a qualitative approach adopting the case study research method (Yin, 2003). Data were collected through fifteen semi-structured interviews (a total of twelve hours) with the involved departments (particularly

A Proposed Nonlinear Programming Optimization Model for Optimal Budget Mix of Digital Marketing Campaigns
This paper proposes a nonlinear mathematical model to address the problem of optimizing budget allocation within digital marketing campaigns. The model provides marketers with a systematic quantitative framework for effective budget allocation across various platforms. The model seeks to identify the optimal budget mix that maximizes the expected net impressions using the Sainsbury Normal Method (SNM). The proposed model considers multiple constraints, such as budget limitations and advertiser's preferences. Results demonstrate the applicability of the model through hypothetical two case