
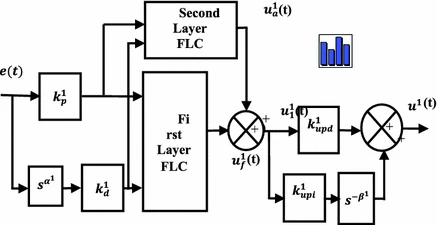
An intelligent adaptive fuzzy logic control technique, Fractional Order Self Organizing Fuzzy Controller (FOSOFC) is presented and applied to control a two link planar electrically-driven rigid robotic (EDRR) manipulator system. As EDRR is a multi-input multi-output complex nonlinear system, an intelligent adaptive controller, FOSOFC is considered to control it perfectly. To show the efficacy of the FOSOFC controller, the obtained performance is compared with fractional order fuzzy proportional integral and derivative (FOFPID) controller for study in servo as well as the regulatory problems

Based on stability theory of linear fractional order systems and stability theory of linear integer order systems, the problem of coexistence of various types of synchronization between different dimensional fractional chaotic systems is investigated in this paper. Numerical and simulation results have clearly shown the effectiveness of the novel approach developed herein. © 2018, Springer International Publishing AG.
The integration of biometric recognition with smartphones is necessary to increase security, especially in financial transactions such as online payments. Vein recognition of the dorsal hand is superior to other methods such as palm, finger, and wrist, as it has a wide area to be captured and does not have any wrinkles. Most current systems that depend on dorsal hand vein recognition do not work in real-time and have poor results. In this paper, a dorsal hand recognition system working in real-time is proposed to achieve good results with a high frame rate. A contactless device consists of a
System Verilog Assertions (SVA) is widely used by hardware designers and verification engineers to apply Assertion Based Verification (ABV) methodology on their hardware designs. However, the complexity in understanding different protocol standards in general and JEDEC memory protocol standards in specific imposes numerous difficulties on designers and verification engineers when translating design specifications into SVA. This motivated us to devise new techniques that can be used to automatically generate SVA for DDR memory protocols with no ambiguity when capturing design requirements from
Purpose: Tagged and cine magnetic resonance imaging (tMRI and cMRI) techniques are used for evaluating regional and global heart function, respectively. Measuring global function parameters directly from tMRI is challenging due to the obstruction of the anatomical structure by the tagging pattern. The purpose of this study was to develop a method for processing the tMRI images to improve the myocardium-blood contrast in order to estimate global function parameters from the processed images. Materials and methods: The developed method consists of two stages: (1) removing the tagging pattern
The aim of this paper is to develop a functional approach to optimize the engagement effectiveness of the tactical homing missiles and air defense systems by utilizing the differential geometric concepts. In this paper the engagement geometry of the interceptor and the target is developed and expressed in differential geometric terms in order to demonstrate the possibilities of the impact triangles and specify the earliest interception based on the direct intercept geometry. Optimizing the missile heading angle and suitable missile velocity against the target velocity is then examined to
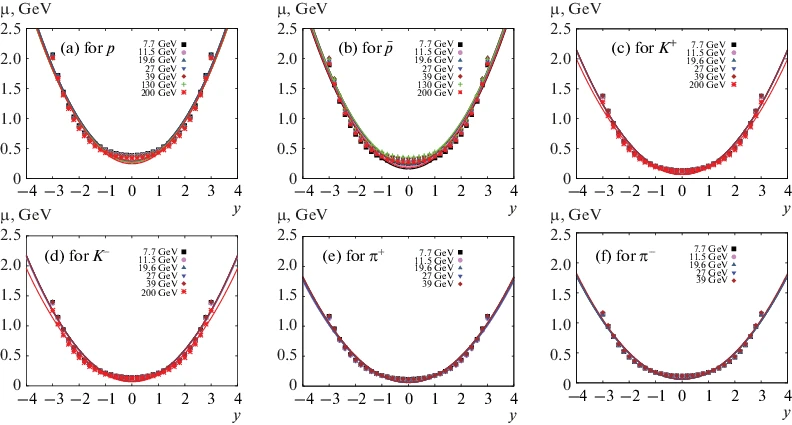
Abstract: Based on statistical thermal approaches, the transverse momentum distribution of the well-identified produced particles, π+, π–, K+, K–, p, and (Fromula presented.), is studied. We aim at introducing a novel almost entirely empirical estimation for the inclusive chemical potential μ. From the partition function of a grand-canonical ensemble, we propose a generic expression for the dependence of μ on the rapidity y. Then, by fitting this expression with the experimental results of the most central p⊥ and d2N/2πp⊥dp⊥dy, at 7.7, 11.5, 19.6, 27, 39, 130, 200 GeV, we introduce a generic
The proposed correspondence between the Hawking-Unruh radiation mechanism in rotating, electrically-charged, and electrically-charged-rotating black holes and the hadronization process in high-energy collisions is assumed here. This allows us to determine the well-profound freezeout parameters characterizing the heavy-ion collisions. Furthermore, black holes thermodynamics is found analogous to a to that of the high-energy collisions. We also introduce a relation expressing the dependence of the angular momentum and the angular velocity deduced from rotating black holes on the chemical
Background: Lung cancer is a leading cause of cancer-related death worldwide and is the most commonly diagnosed cancer. Like other cancers, it is a complex and highly heterogeneous disease involving multiple signaling pathways. Identifying potential therapeutic targets is critical for the development of effective treatment strategies. Methods: We used a systems biology approach to identify potential key regulatory factors in smoking-induced lung cancer. We first identified genes that were differentially expressed between smokers with normal lungs and those with cancerous lungs, then integrated
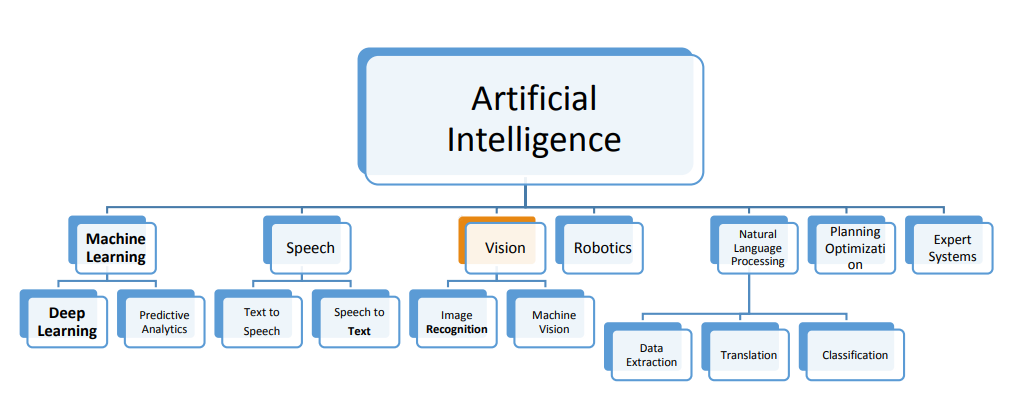
In the era of digital transformation, a mass disruption in the global industries have been detected. Big data, the Internet of Things (IoT) and Artificial Intelligence (AI) are just examples of technologies that are holding such digital disruptive power. On the other hand, retailing is a high-intensity competition and disruptive industry driving the global economy and the second largest globally in employment after the agriculture. AI has large potential to contribute to global economic activity and the biggest sector gains would be in retail. AI is the engine that is poised to drive the