
Purpose - The purpose of this paper is to present a dynamic model to measure the degree of system's leanness under dynamic demand conditions using a novel integrated metric. Design/methodology/approach - The multi-stage production system model is based on a system dynamics approach. The leanness level is measured using a new developed integrated metric that combines efficiency,WIP performance as well as service level. The analysis includes design of experiment technique at the initial analysis to examine the most significant parameters impacting the leanness score and then followed by
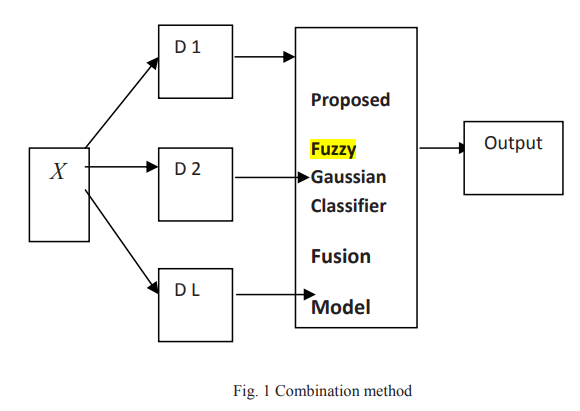
In the field of pattern recognition multiple classifier systems based on the combination of outputs from different classifiers have been proposed as a method of high performance classification systems. The objective of this work is to develop a fuzzy Gaussian classifier for combining multiple learners, we use a fuzzy Gaussian model to combine the outputs obtained from K-nearest neighbor classifier (KNN), Fuzzy K-nearest neighbor classifier and Multi-layer Perceptron (MLP) and then compare the results with Fuzzy Integral, Decision Templates, Weighted Majority, Majority Naïve Bayes, Maximum
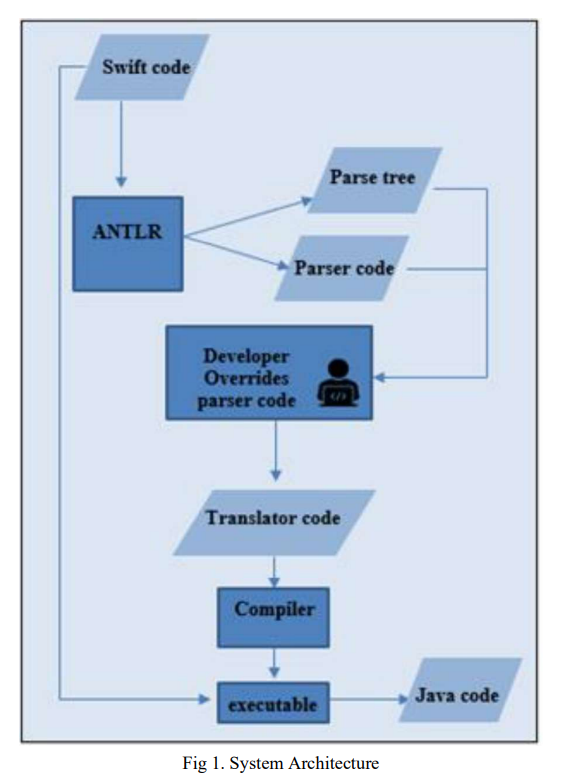
Numerous commercial tools like Xamarin, React Native and PhoneGap utilize the concept of cross-platform mobile applications development that builds applications once and runs it everywhere opposed to native mobile app development that writes in a specific programming language for every platform. These commercial tools are not very efficient for native developers as mobile applications must be written in specific language and they need the usage of specific frameworks. In this paper, a suggested approach in TCAIOSC tool to convert mobile applications from Android to iOS is used to develop the
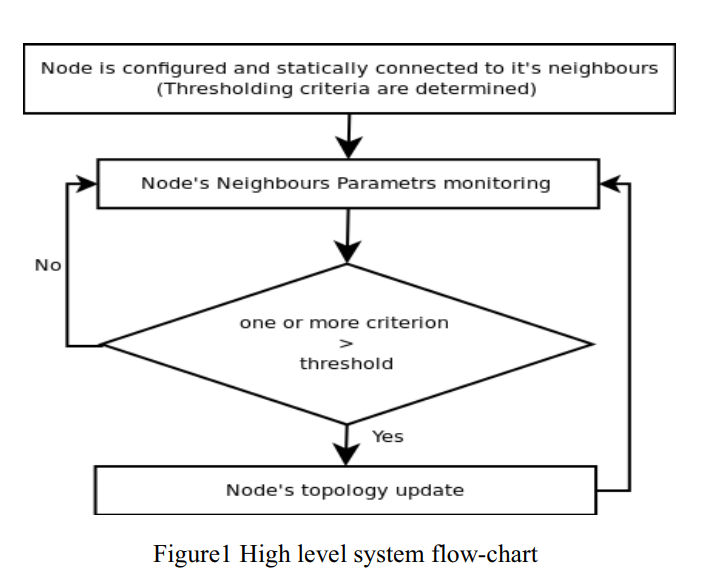
Ad hoc networks are peer mobile nodes that self configure to form a network. In these types of networks there is no routing infrastructure, and usually nodes have limited resources. This imposes a serious problem due to some nodes' selfishness and willingness to preserve their resources. Many approaches have been proposed to deal with this problem and mitigate the selfishness; amongst these approaches are reputation systems. This paper proposes a reputation system scheme that helps isolating misbehaving nodes and decreasing their ability to launch an attack on the network. The idea of this
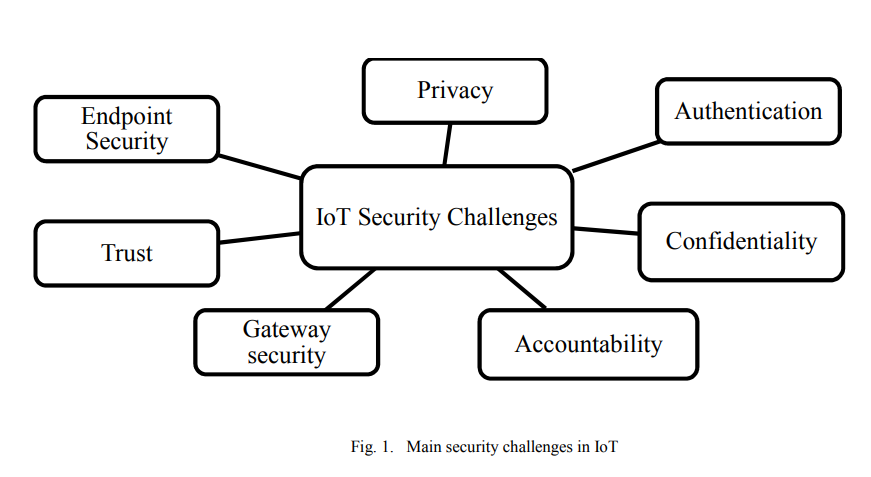
For the past decade, Internet of Things (IoT) had an important role in our lives. It connects a large number of embedded devices. These devices fulfill very difficult and complicated tasks, which facilitate our work. Till now the security of IoT faces many challenges such as privacy, authentication, confidentiality, trust, middleware security, mobile security and policy enforcement. In order to provide a secure environment for IoT, this paper proposes a framework for IoT devices. © 2017 IEEE.
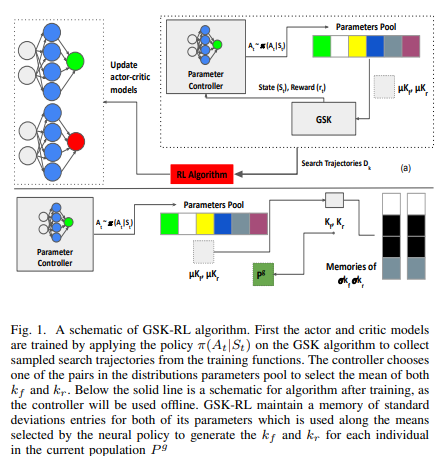
Meta-heuristics and nature inspired algorithms have been prominent solvers for highly complex, nonlinear and hard optimization problems. The Gaining-Sharing Knowledge algorithm (GSK) is a recently proposed nature-inspired algorithm, inspired by human and their tendency towards growth and gaining and sharing knowledge with others. The GSK algorithm have been applied to different optimization problems and proved robustness compared to other nature-inspired algorithms. The GSK algorithm has two main control parameters kfand kr which controls how much individuals gain and share knowledge with
The rise of the Internet of Things (IoT) has led to a numerous and diverse amount of products and real life implementations for smart cities in the last few years. With the many opportunities and challenges, the academic and industrial field has come up with many hardware and middleware platforms. We categorise these different IoT applications and solutions into different domains and present an application for each. This survey aims at defining the state-of-the-art major and common technologies, frameworks, and applications used to open doors to drive future research and to spark new ideas for
Building a system to extract Arabic named entities is a complex task due to the ambiguity and structure of Arabic text. Previous approaches that have tackled the problem of Arabic named entity recognition relied heavily on Arabic parsers and taggers combined with a huge set of gazetteers and sometimes large training sets to solve the ambiguity problem. But while these approaches are applicable to modern standard Arabic (MSA) text, they cannot handle colloquial Arabic. With the rapid increase in online social media usage by Arabic speakers, it is important to build an Arabic named entity
Intelligent camera systems provide an effective solution for road traffic monitoring with traffic stream characteristics, such as volumes and densities, continuously computed and relayed to control stations. However, developing a functional vision-based traffic monitoring system is a complex task that entails the creation of appropriate visual sensing platforms with on-board visual analytics algorithms, integration of versatile technologies for data provision and stream management, and development of data visualization techniques suitable for end-users. This paper describes TraffiSense, a
As the common understanding of Cloud Computing is continuously evolving, the terminology and concepts used to define it often need clarifying. Therefore, Cloud customers and Cloud Providers are used to dispute about Service Level Agreements, Service Level Objectives and Quality of Service. Simultaneously, SLAs/SLOs/QoS represent other related technical problems such as Security, Privacy, Compliancy and others. Technical problems are usually defined within technical context, where both parties ignore analyzing problem's legally related causes. In fact, these problems are stemming from the