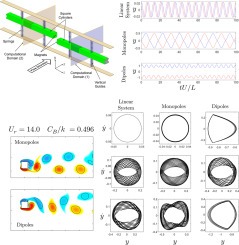
A square cylinder may gallop if subjected to fluid flow, experiencing a self-excited vibration mode that can harvest energy for low-power applications. The harvested power is typically low and depends on the upstream flow velocity and system dynamic parameters. In this study, the influence of nonlinear stiffness induced by two repulsive magnetic poles on the galloping response of square rods is investigated at a mass ratio of 10 and a Reynolds number of 200. The vibration response of two identical coaxial square rods with magnetic poles attached to their opposite ends is analyzed. Two

Underactuated robots are intriguing systems that have found numerous applications across various fields. These systems are characterized by having fewer actuators than degrees of freedom, resulting in complex behaviors that challenge traditional modeling and control techniques. Despite the prevalent use of data-driven modeling, extracting the dynamic model of underactuated systems is particularly challenging. This paper focuses on deriving from data the dynamic model of the Double Inverted Pendulum on a Cart (DIPC). The Euler-Lagrange equations are employed to derive the model's terms from the

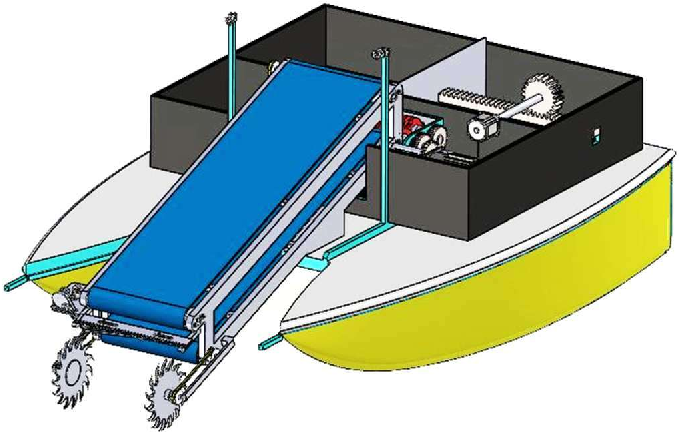
Water hyacinth has become widespread in freshwater bodies in several countries, leading to various issues, particularly its substantial water consumption and the resulting need to control its growth. Among the different methods of controlling water hyacinth, mechanical control stands out as the most effective and environmentally friendly approach. A proposed harvester robot has been developed, capable of efficiently cutting and collecting water hyacinth from the water's surface. The robot boasts several advantages, including its ability to operate in narrow water paths and lakes, use clean

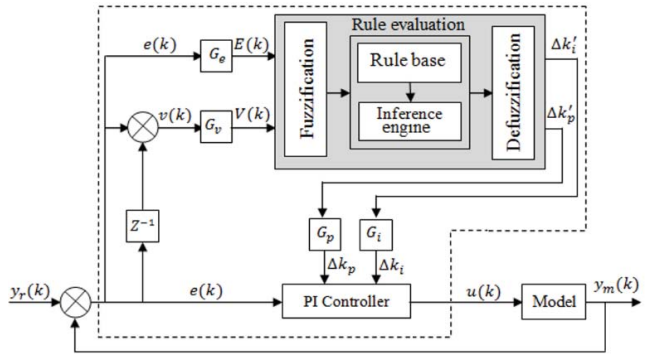
This paper is dedicated to design a fuzzy-supervised PI controller. It is a is a two-level controller, the lower-level controller (LLC) containing the classical PI controller and the upper-level controller (ULC) is a supervisory fuzzy logic controller (FLC). In real time, the ULC modifies, automatically, the parameters of the LLC which, consequently, drive the process to the desired status. The performance of the proposed controller is, primarily, examined by simulating it in MATLAB. Then, it is experimentally validated and compared to the classical PI-control through two test phases, the

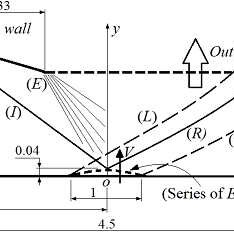
The shock wave boundary layer interaction (SW-BLI) phenomenon over transonic and supersonic airfoils captured the attention of aerospace engineers, due to its disastrous effect on the aerodynamic performance of these vehicles. Thus, the scientific community numerically and experimentally investigated several active and passive flow control elements to reduce the effect of the phenomenon, such as vortex generator, cavity, and bump. They focused on designing and optimizing the shape and location of the bump control element. However, the transit movement of the bump from the state of a clean

The contribution of the present work is to develop a simple, yet efficient, capturing technique to be used with flapping wings during numerical simulation using Eulerian grids. The developed technique is based on the simplicity of the geometry of the flapping wing model. The results of the proposed technique are successfully compared with other well-known capturing techniques namely, Sum of Angles and Modified Polygon techniques. The developed technique also showed that it can lower the running time into half. © 2022 IEEE.

Starting with the simple geometry of a flat plate to study the transient phase of the morphing Shock Control Bump (SCB), this paper presents the results of the second phase of our investigation. The SCB is morphed with different velocity profiles at the optimal morphing time from our previous study. Five motion profiles are tested to morph the SCB, namely; linearmotion, parabolic motion, half-parabolic motion, reversed parabolic motion, and half-reversed parabolic motion. The aim of this paper is to numerically determine the suitable velocity profile that minimizes the entropy losses, the lag

Many applications in our everyday living are totally depending on using the robots. So that, the need for having smart and more productive robots is increasing. Developing such robots necessitates the programming of the robot. Hence, the machine learning approaches are widely employed to accomplish this objective successfully. Programming the robot can be applied by demonstration such that the skills are transferred to robots through supplying examples of the desired movement. Multiple trajectories are observed and modelled in order to learn new skills by obtaining a general trajectory of the

Corrosion of steel reinforcement is reason of many deteriorations in RC structures especially in coastal areas. Thus, the conventional steel rebars should be replaced by other alternatives to mitigate this phenomenon, consequently, enhance the durability of structures. In this article, combined utilization of glass fiber reinforced polymer (GFRP) and stainless-steel (SS) is proposed as a substitute of traditional steel. To provide adequate strength and ductility with acceptable cost, GFRP is utilized as distributed and concentrated reinforcement overall wall, while SS is partially used as

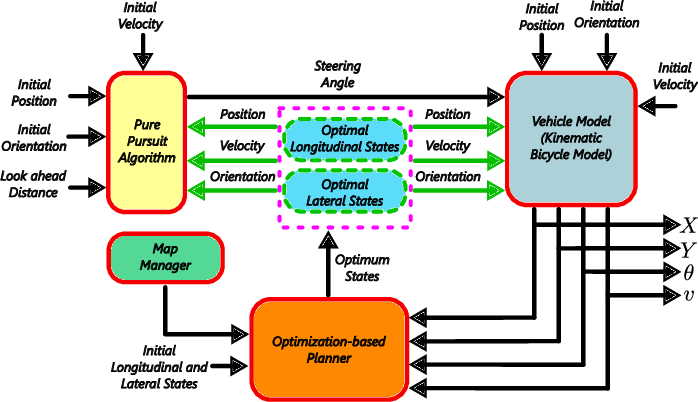
Autonomous Vehicles (AVs) are critical, and nowadays are essential technology that transfers traditional transportation systems into smart, and driverless ones. Considering the available processed data and information that came from localization, perception, and HD map, AVs could exceed the limit of the efficiency and safety of those conventional systems. AVs could use enhanced techniques and algorithms to execute safety-critical scenarios in dynamic environments that have static and dynamic obstacles, traffic signs,..., etc. This paper aims to propose a novel motion planning algorithm that