Single and dual solutions of fractional order differential equations based on controlled Picard's method with Simpson rule
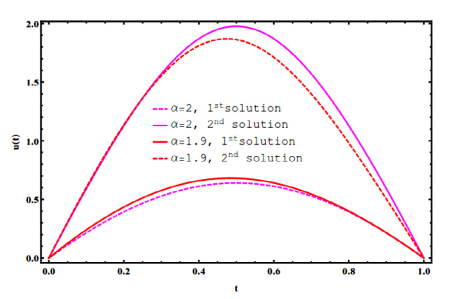
This paper presents a semi-analytical method for solving fractional differential equations with strong terms like (exp, sin, cos,…). An auxiliary parameter is introduced into the well-known Picard's method and so called controlled Picard's method. The proposed approach is based on a combination of controlled Picard's method with Simpson rule. This approach can cover a wider range of integer and fractional orders differential equations due to the extra auxiliary parameter which enhances the convergence and is suitable for higher order differential equations. The proposed approach can be effectively applied to Bratu's problem in fractional order domain to predict and calculate all branches of problem solutions simultaneously. Also, it is tested on other fractional differential equations like nonlinear fractional order Sine-Gordon equation. The results demonstrate reliability, simplicity and efficiency of the approach developed. © 2017 University of Bahrain