Quantification of memory in fractional-order capacitors
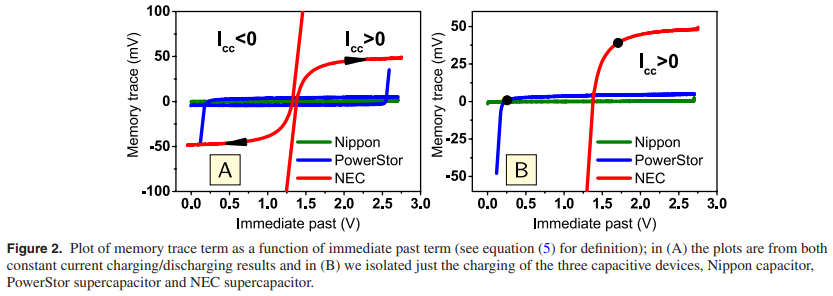
In this study we quantify and interpret the inherent memory in fractional-order capacitors when subjected to constant current charging/discharging waveforms. This is done via a finite difference approximation of the fractional order rate equation I(t) = Cαdαv(t)/dtα (0 le; α ≤ 1) relating current to voltage in these devices. It is found that as the fractional exponent α decreases, the weight of the voltage memory trace that results from the contribution of past voltage activity increases, and thus the measured response of the device at any time is increasingly correlated to its past. Ideal capacitors, on the other hand, which are described by the first order differential equation I(t) = Cdv(t)/dt, do not exhibit such behavior and are memoryless devices. © 2019 IOP Publishing Ltd.