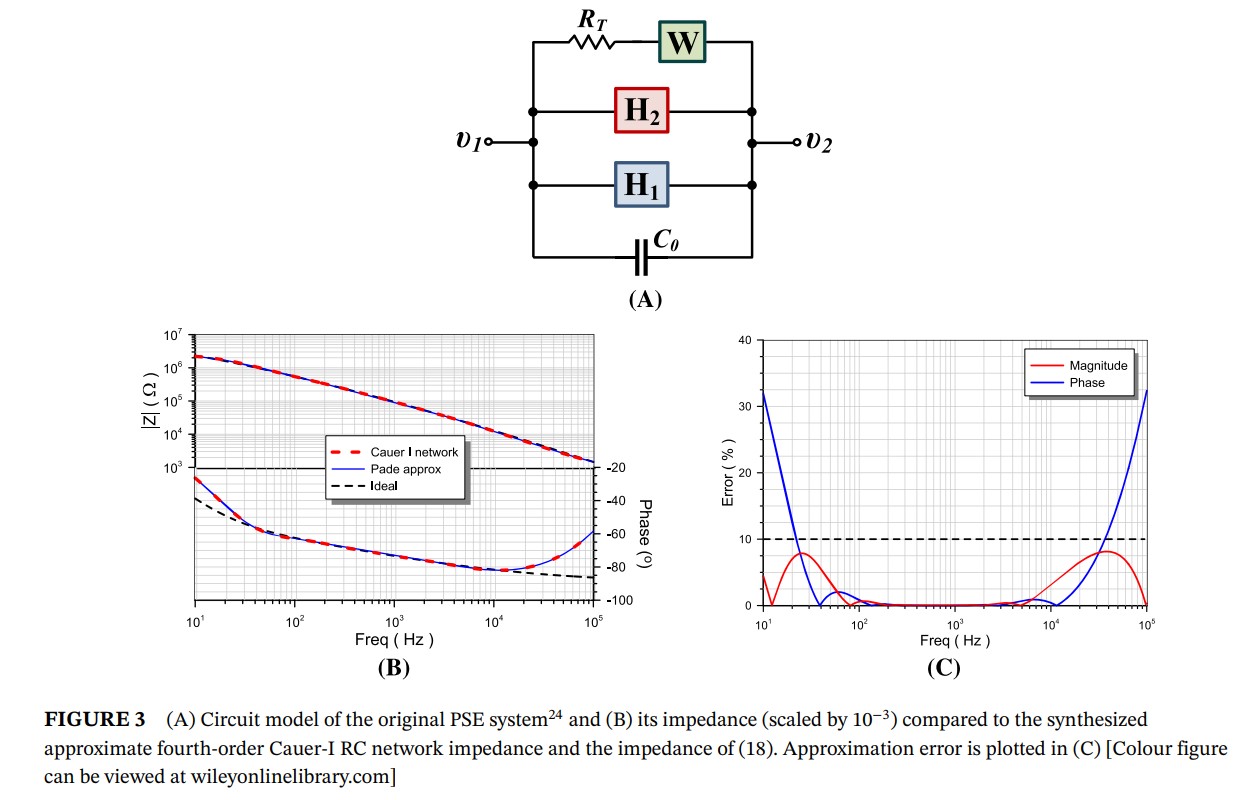
Passive approximations of double-exponent fractional-order impedance functions
Double-exponent fractional-order impedance functions are important for modeling a wide range of biochemical materials and biological tissues. Through appropriate selection of the two exponents (fractional orders), the well-known Havriliak–Negami, Cole–Cole, Cole–Davidson, and Debye relaxation models can be obtained as special cases. Here we show that an integer-order Padé-based approximation of the Havriliak–Negami function is possible to obtain and can be realized using appropriately configured Cauer/Foster resistor-capacitor (RC) networks. Two application examples are subsequently examined: the emulation of the capacitive behavior in a polycrystalline solid electrolyte and the emulation of the impedance of four “fractal” vegetable types. © 2021 John Wiley & Sons, Ltd.