A novel 4-D hyperchaotic system with two quadratic nonlinearities and its adaptive synchronisation

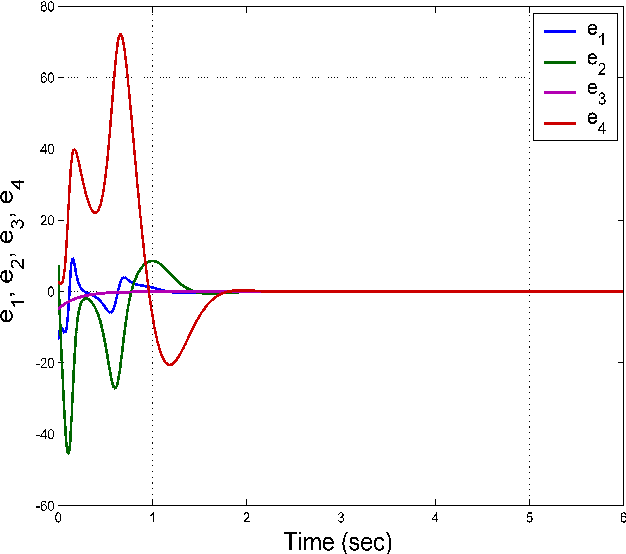
This work announces an eleven-term novel 4-D hyperchaotic system with two quadratic nonlinearities. A qualitative analysis of the properties of the novel 4-D hyperchaotic system is presented. A special feature of our novel hyperchaotic system is that it has three equilibrium points of which two are unstable and one is locally asymptotically stable. The Lyapunov exponents of the novel hyperchaotic system are obtained as L1 = 1.5146, L2 = 0.2527, L3 = 0 and L4 = −12.7626. The Kaplan-Yorke dimension of the novel hyperchaotic system is derived as DKY = 3.1385. Next, this work describes the design of an adaptive controller for the global hyperchaos synchronisation of identical novel hyperchaotic systems with unknown parameters. MATLAB simulations are shown to describe all the main results derived in this work. Copyright © 2018 Inderscience Enterprises Ltd.