Design and implementation of a simple dynamical 4-D chaotic circuit with applications in image encryption

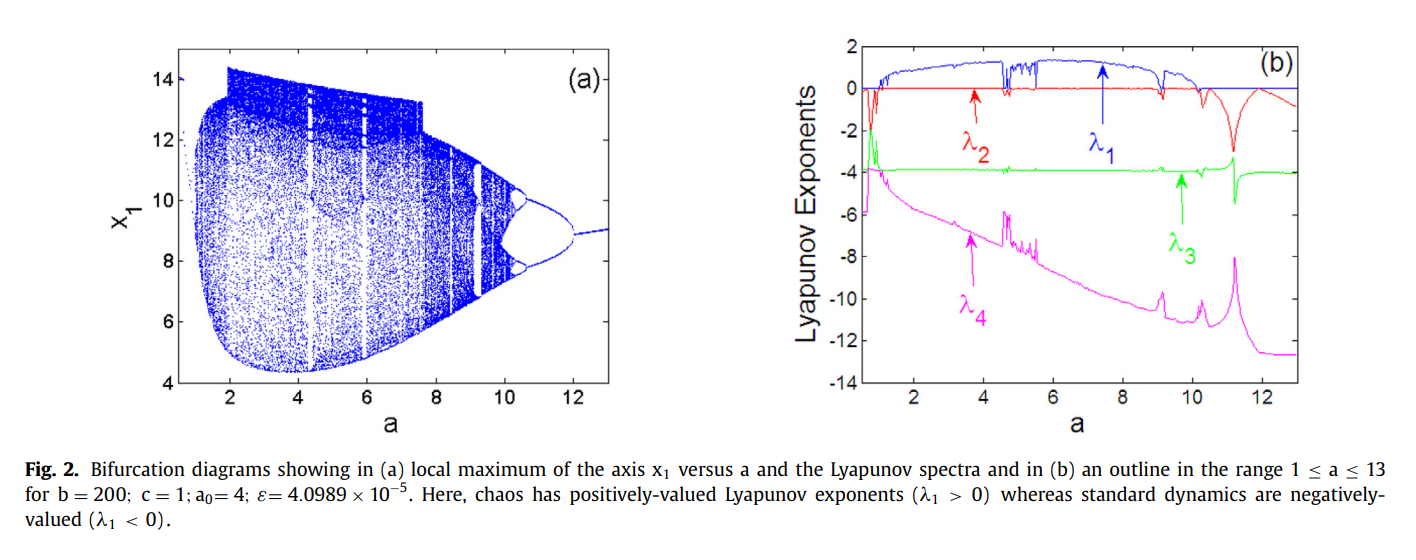
We present a simple yet highly dimensional hybrid diode bridge circuit network that can exhibit complex chaotic behaviours. Further, since our network is characterised by smooth fourth-order exponential nonlinearity, we employ a distinctive approach to assess its different properties: we examine the circuit stability near fixed points. Specifically, we evaluate dynamic complexity using the Lyaponov spectrum analysis, bifurcation analysis and phase space trajectories; additionally, we assess coexisting attractors in the parameter space using numerical and experimental analysis. Furthermore, we report assessments of our network in terms of remerging Feigenbaum trees and metastable chaos. Finally, these properties, and especially the chaotic series of the coexisting attractors, were exploited to implement a chaos-based image encryption protocol using S-box construction and PRNG generation mechanisms. To validate the performance of our protocol, we employed standard security analysis including correlation coefficient, pixel change rate, information entropy, time complexity and key space analysis whose outcome were compared alongside available state-of-the-art methods. Outcomes suggest promising applications for our chaotic circuit network in image encryption. © 2019