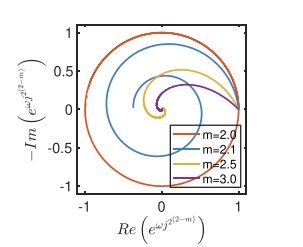
Decoupling the magnitude and phase in a constant phase element
The success of fractional-order fractance (FOF) as a modeling tool in (photo)bio(electro)chemical systems can be readily gauged by the large body of research work that has been conducted over the past few years in terms of materials fabrication, building integer-order emulators of their behavior, as well as applications in filter design, controller design, modeling of energy storage devices and biomaterials. The impedance of FOF has the general form Zα(s)=kαsα where kα and α are real constant and s=jω is the complex Laplace number. In this work, we investigate the possibility of decoupling the magnitude and phase properties of a FOF, and the application of this modified circuit element in the modeling of spectral electrochemical data. The proposed modification relies on the complex parametric function jβωα=jβ-αsα which can been viewed as a phase-shifted version of sα=(jω)α by a β-dependent constant angle. This extra degree of freedom is expected to be useful in facilitating the modeling of more complex systems in which the classical FOF fails, and is here verified on the low-frequency response of a lithium-ion battery showing unstationary and/or nonlinear behavior. © 2021 Elsevier B.V.