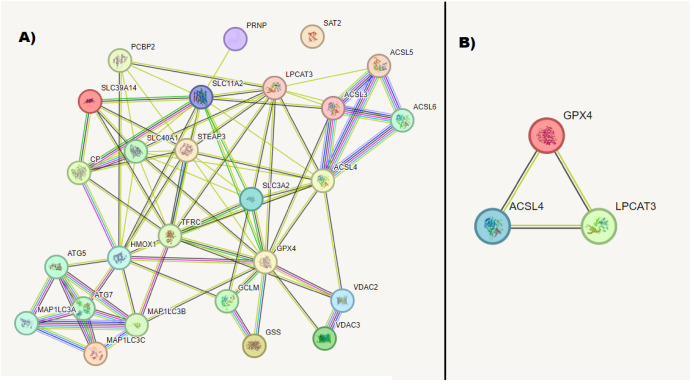
The water-filling game in fading multiple-access channels
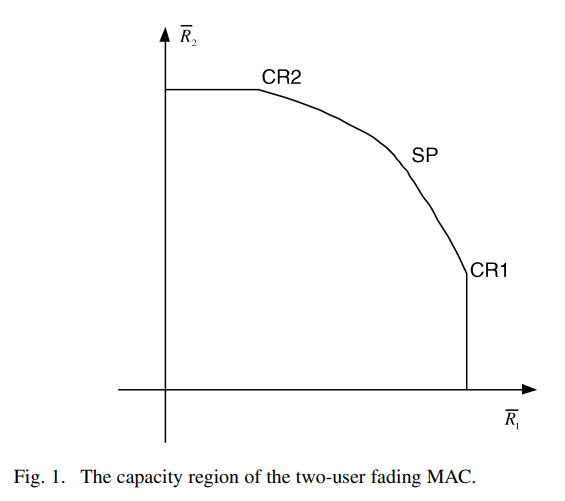
A game-theoretic framework is developed to design and analyze the resource allocation algorithms in fading multiple-access channels (MACs), where the users are assumed to be selfish, rational, and limited by average power constraints. The maximum sum-rate point on the boundary of the MAC capacity region is shown to be the unique Nash equilibrium of the corresponding water-filling game. This result sheds a new light on the opportunistic communication principle. The base station is then introduced as a player interested in maximizing a weighted sum of the individual rates. A Stackelberg formulation is proposed in which the base station is the designated game leader. In this setup, the base station announces first its strategy defined as the decoding order of the different users, in the successive cancellation receiver, as a function of the channel state. In the second stage, the users compete conditioned on this particular decoding strategy. This formulation is shown to be able to achieve all the corner points of the capacity region, in addition to the maximum sum-rate point. On the negative side, it is shown that there does not exist a base station strategy in this formulation that achieves the rest of the boundary points. To overcome this limitation, a repeated game approach, which achieves the capacity region of the fading MAC, is presented. Finally, the study is extended to vector channels highlighting interesting differences between this scenario and the scalar channel case. © 2008 IEEE.